
科目: 来源: 题型:
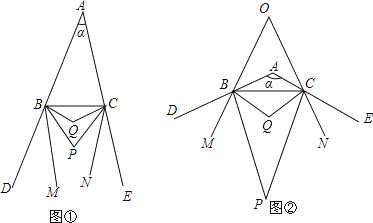
【题目】已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC= °,∠BQC= °;
(2)当α= °时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系: .
查看答案和解析>>
科目: 来源: 题型:
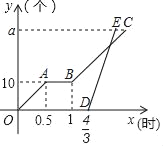
【题目】甲、乙两名工人分别加工a个同种零件.甲先加工一段时间,由于机器故障进行维修后继续按原来的工作效率进行加工,当甲加工![]() 小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
小时后.乙开始加工,乙的工作效率是甲的工作效率的3倍.下图分别表示甲、乙加工零件的数量y(个)与甲工作时间x(时)的函数图象.解读信息:
(1)甲的工作效率为 个/时,维修机器用了 小时
(2)乙的工作效率是 个/时;问题解决:
①乙加工多长时间与甲加工的零件数量相同,并求此时乙加工零件的个数;
②若乙比甲早10分钟完成任务,求a的值.
查看答案和解析>>
科目: 来源: 题型:
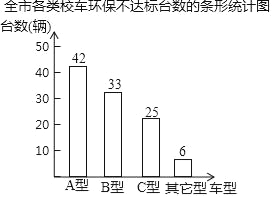
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目: 来源: 题型:
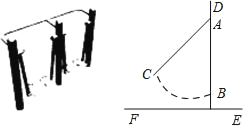
【题目】图1中是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,从侧面看图2,立柱DE高1.7m,AD长0.3m,踏板静止时从侧面看与AE上点B重合,BE长0.2m,当踏板旋转到C处时,测得∠CAB=42°,求此时点C距离地面EF的高度.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
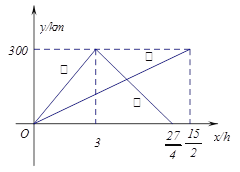
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛(满分100分),如下表所示:
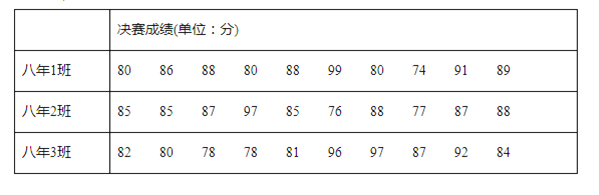
解答下列问题:
(1)请填写下表:
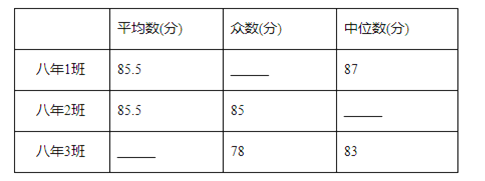
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好);
②从平均数和中位数相结合看(分析哪个班级成绩好);
(3)如果在每个班级参加决赛的选手中选出3人参加总决赛,你认为哪个班级的实力更强一些,请简要说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
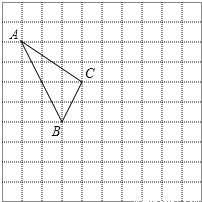
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)写出点B的坐标;
(3)将△ABC向右平移5个单位长度,向下平移2个单位长度,画出平移后的图形△A′B′C′;
(4)计算△A′B′C′的面积﹒
(5)在x轴上存在一点P,使PA+PC最小,直接写出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图所示,直线y=-![]() x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
x+3与坐标轴分别交于点A,B,与直线y=x交于点C,线段OA上的点Q以每秒1个单位的速度从点O出发向点A作匀速运动,运动时间为t秒,连结CQ.
(1)求出点C的坐标;
(2)若△OQC是等腰直角三角形,则t的值为________;
(3)若CQ平分△OAC的面积,求直线CQ对应的函数表达式.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.

(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com