
科目: 来源: 题型:
【题目】如图,点A在直线l上,点B在直线l外,点B关于直线l的对称点为C,连接AC,过点B作BD⊥AC于点D,延长BD至E使BE=AB,连接AE并延长与BC的延长线交于点F.

(1)补全图形;
(2)若∠BAC=2α,求出∠AEB的大小(用含α的式子表示);
(3)用等式表示线段EF与BC的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②a-b+c>0;③ 2a+b=0;④b2-4ac>0 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有()

A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】我们规定在网格内的某点进行一定条件操作到达目标点:H代表所有的水平移动,H1代表向右水平移动1个单位长度,H-1代表向左平移1个单位长度;S代表上下移动,S1代表向上移动1个单位长度,S-1代表向下移动1个单位长度,![]() 表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;
表示点P在网格内先一次性水平移动,在此基础上再一次性上下移动;![]() 表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
表示点P在网格内先一次性上下移动,在此基础上再一次性水平移动.
(1)如图,在网格中标出![]() 移动后所到达的目标点
移动后所到达的目标点![]() ;
;

(2)如图,在网格中的点B到达目标点A,写出点B的移动方法________________;

(3)如图,在网格内有格点线段AC,现需要由点A出发,到达目标点D,使得A、C、D三点构成的格点三角形是等腰直角三角形,在图中标出所有符合条件的点D的位置并写出点A的移动方法.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边三角形ABC右侧作射线CP,∠ACP=![]() (0°<
(0°<![]() <60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.
<60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.

(1)求∠DBC的大小(用含![]() 的代数式表示);
的代数式表示);
(2)在![]() (0°<
(0°<![]() <60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.
(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.
①写出∠MDA= °,AB的长是 .
②求四边形AMDN的周长;

(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,连接
边上,连接![]() ,连接
,连接![]()

(1)求证:![]()
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]()
①补全图形并证明![]()
②利用备用图进行画图、试验、探究,找出当![]() 三点恰好共线时点
三点恰好共线时点![]() 的位置,请直接写出此时
的位置,请直接写出此时![]() 的度数,并画出相应的图形
的度数,并画出相应的图形
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() (
(![]() ,
,![]() 、
、![]() 、
、![]() 为常数)的图象如图所示,下列
为常数)的图象如图所示,下列![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 为常数,且
为常数,且![]() .其中正确的结论有( )
.其中正确的结论有( )
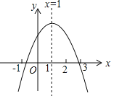
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目: 来源: 题型:
【题目】对于△ABC及其边上的点P,给出如下定义:如果点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 都在△ABC的边上,且
都在△ABC的边上,且![]() ,那么称点
,那么称点![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距点,线段
为△ABC关于点P的等距点,线段![]() ,
,![]() ,
,![]() ,……,
,……,![]() 为△ABC关于点P的等距线段.
为△ABC关于点P的等距线段.
(1)如图1,△ABC中,∠A<90°,AB=AC,点P是BC的中点.

①点B,C △ABC关于点P的等距点,线段PA,PB △ABC关于点P的等距线段;(填“是”或“不是”)
②△ABC关于点P的两个等距点![]() ,
,![]() 分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段
分别在边AB,AC上,当相应的等距线段最短时,在图1中画出线段![]() ,
,![]() ;
;
(2)△ABC是边长为4的等边三角形,点P在BC上,点C,D是△ABC关于点P的等距点,且PC=1,求线段DC的长;
(3)如图2,在Rt△ABC中,∠C=90°,∠B=30°.点P在BC上,△ABC关于点P的等距点恰好有四个,且其中一个是点![]() .若
.若![]() ,直接写出
,直接写出![]() 长的取值范围.(用含
长的取值范围.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com