
科目: 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
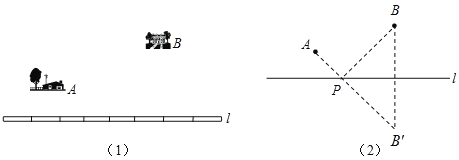
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
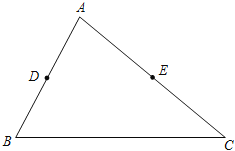
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD,CE分别是AC,AB边上的高,BD, CE交于O,则图中共有相似三角形( )

A. 5对 B. 6对 C. 7对 D. 8对
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.如图①、②、③,正三角形
上逆时针运动.如图①、②、③,正三角形![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 分别是
分别是![]() 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 开始,以相同的速度中
开始,以相同的速度中![]() 上逆时针运动.
上逆时针运动.
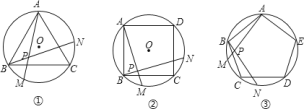
(1)求图①中![]() 的度数;
的度数;
(2)图②中,![]() 的度数是________,图③中
的度数是________,图③中![]() 的度数是________;
的度数是________;
(3)根据前面探索,你能否将本题推广到一般的正![]() 边形情况?若能,写出推广问题和结论;若不能,请说明理由.
边形情况?若能,写出推广问题和结论;若不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
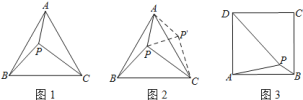
小伟遇到这样一个问题:如图![]() ,在正三角形
,在正三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图![]() ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造![]() ,连接
,连接![]() ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
(1)请你回答:图![]() 中
中![]() 的度数等于________.
的度数等于________.
参考小伟同学思考问题的方法,解决下列问题:
(2)如图![]() ,在正方形
,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数和正方形的边长.
的度数和正方形的边长.
查看答案和解析>>
科目: 来源: 题型:
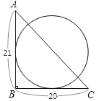
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .若有一半径为
.若有一半径为![]() 的圆分别与
的圆分别与![]() 、
、![]() 相切,则下列何种方法可找到此圆的圆心( )
相切,则下列何种方法可找到此圆的圆心( )
A. ![]() 的角平分线与
的角平分线与![]() 的交点 B.
的交点 B. ![]() 的中垂线与
的中垂线与![]() 中垂线的交点
中垂线的交点
C. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点 D.
中垂线的交点 D. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点
中垂线的交点
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知在平面直角坐标系中,A(![]() ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=![]() .
.

(1)求直线AD的解析式和线段BD所在直线的解析式.
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一个三位正整数n各数位上的数字重新排列(含n本身)后,得到新的三位数![]() (a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称
(a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称![]() 是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称
是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称![]() 是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=
是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=![]() 是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=
是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=![]() .
.
(1)计算:F(168),G(168);
(2)设三位自然数s=100x+50+y(1≤x≤9,1≤y≤9,且x,y均为正整数),交换其个位上的数字与百位上的数字得到t,若s﹣t=693,那么我们称s为“厚积薄发数”;请求出所有“厚积薄发数”中M(s)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com