
科目: 来源: 题型:
【题目】甲、乙两人参加某体育项目训练,为了便于研究,把最后5次的训练成绩分别用实线和虚线连接起来,如图,下面的结论错误的是( )

A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试,甲的成绩与乙的成绩相同
C. 第4次测试,甲的成绩比乙的成绩多2分
D. 在5次测试中,甲的成绩都比乙的成绩高
查看答案和解析>>
科目: 来源: 题型:
【题目】改革开放40年以来,城乡居民生活水平持续快速提升,居民教育、文化和娱乐消费支出持续增长,已经成为居民各项消费支出中仅次于居住、食品烟酒、交通通信后的第四大消费支出,如图为北京市统计局发布的2017年和2018年我市居民人均教育、文化和娱乐消费支出的折线图.

说明:在统计学中,同比是指本期统计数据与上一年同期统计数据相比较,例如2018年第二季度与2017年第二季度相比较;环比是指本期统计数据与上期统计数据相比较,例如2018年第二季度与2018年第一季度相比较.
根据上述信息,下列结论中错误的是( )
A. 2017年第二季度环比有所提高
B. 2017年第三季度环比有所提高
C. 2018年第一季度同比有所提高
D. 2018年第四季度同比有所提高
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1、2、3分别表示甲、乙、丙三人由A地到B地的路线图,已知
甲的路线为:A→C→B;
乙的路线为:A→D→E→F→B,其中E为AB的中点;
丙的路线为:A→I→J→K→B,其中J在AB上,且AJ>JB.

若符号[→]表示[直线前进],则根据图1、图2、图3的数据,判断三人行进路线长度的大小关系为( )
A. 甲=乙=丙 B. 甲<乙<丙 C. 乙<丙<甲 D. 丙<乙<甲
查看答案和解析>>
科目: 来源: 题型:
【题目】如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图(两图都不完整),下列结论错误的是( )

A. 该班总人数为50人B. 步行人数为30人
C. 乘车人数是骑车人数的2.5倍D. 骑车人数占20%
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,AB=6,BC=8,点E为BC延长线上一点,且BD=BE,连接DE,Q为DE的中点,有一动点P从B点出发,沿BC以每秒1个单位的速度向E点运动,运动时间为t秒.
(1)如图1,连接DP、PQ,则S△DPQ=_____(用含t的式子表示);
(2)如图2,M、N分别为AB、AD的中点,当t为何值时,四边形MNQP为平行四边形?请说明理由;
(3)如图3,连接CQ,AQ,试判断AQ、CQ的位置关系并加以证明.
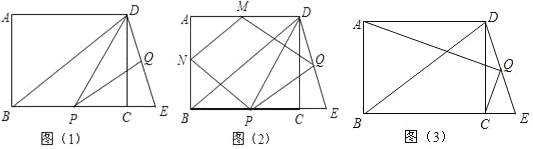
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;
(2)如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;
(3)若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。


查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 如图一:小明想测量一棵树的高度
如图一:小明想测量一棵树的高度![]() ,在阳光下,小明测得一根与地面垂直、长为
,在阳光下,小明测得一根与地面垂直、长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长![]() 为
为![]() 米,落在地面上的影长
米,落在地面上的影长![]() 为
为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
![]() 如图二:在阳光下,小明在某一时刻测得与地面垂直、长为
如图二:在阳光下,小明在某一时刻测得与地面垂直、长为![]() 的杆子在地面上的影子长为
的杆子在地面上的影子长为![]() ,在斜坡上影长为
,在斜坡上影长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,求电线杆的高度.
,求电线杆的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读,再解决问题.
阅读:材料一配方法可用来解一元二次方程.例如,对于方程![]() 可先配方
可先配方![]() ,然后再利用直接开平方法求解方程.其实,配方还可以用它来解决很多问题.
,然后再利用直接开平方法求解方程.其实,配方还可以用它来解决很多问题.
材料二对于代数式![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 有最小值
有最小值![]() ,且当
,且当![]() 时,
时,![]() 取得最小值为
取得最小值为![]() .
.
类似地,对于代数式![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即![]() 有最大值
有最大值![]() ,且当
,且当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.
解答下列问题:
![]() 填空:①当
填空:①当![]() ________时,代数式
________时,代数式![]() 有最小值为________;
有最小值为________;
②当![]() ________时,代数式
________时,代数式![]() 有最大值为________.
有最大值为________.
![]() 试求代数式
试求代数式![]() 的最小值,并求出代数式取得最小值时的
的最小值,并求出代数式取得最小值时的![]() 的值.
的值.
(要求写出必要的运算推理过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com