
科目: 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 150 | 175 | ______ | … | ______ |
方式二的总费用(元) | 90 | 135 | ______ | … | ______ |
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
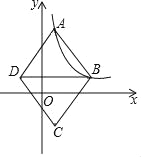
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A是函数y=![]() 图象上的一点,已知B(﹣
图象上的一点,已知B(﹣![]() ,﹣
,﹣![]() ),C(
),C(![]() ,
,![]() ).试利用性质:“y=
).试利用性质:“y=![]() 图象上的任意一点P都满足|PB﹣PC|=2
图象上的任意一点P都满足|PB﹣PC|=2![]() ”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=
”求解下面问题:作∠BAC的内角平分线AE,过B作AE的垂线交AE于F.当点A在函数y=![]() 图象上运动时,点F也总在一图形上运动,该图形为( )
图象上运动时,点F也总在一图形上运动,该图形为( )
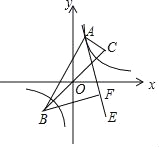
A. 圆 B. 双曲线 C. 抛物线 D. 直线
查看答案和解析>>
科目: 来源: 题型:
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量y(升)与行驶路程x(千米)之间是一次函数关系,其部分图象如图所示.
(1)求y关于x的函数关系式;(不需要写定义域)
(2)已知当油箱中的剩余油量为8升时,该汽车会开始提示加油,在此次行驶过程中,行驶了500千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?

查看答案和解析>>
科目: 来源: 题型:
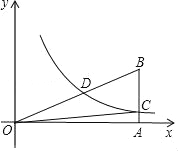
【题目】若关于x的一元二次方程x2+(2k﹣1)x+k2=0的两根a、b满足a2﹣b2=0,双曲线![]() (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),则S△OBC为( )
A. 3 B. ![]() C. 6 D. 3或
C. 6 D. 3或![]()
查看答案和解析>>
科目: 来源: 题型:
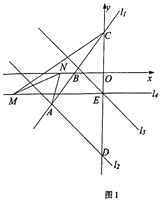
【题目】如图1,在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,已知点
,已知点![]() 的横坐标为-5,直线
的横坐标为-5,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向上平移6个单位得到直线
向上平移6个单位得到直线![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若点
,若点![]() 为垂线
为垂线![]() 上的一个动点,点
上的一个动点,点![]() 为
为![]() 轴上的一个动点,当
轴上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值;
的最小值;
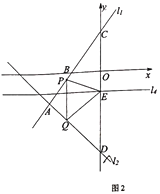
(3)已知点![]() 、
、![]() 分别是直线
分别是直线![]() 、
、![]() 上的两个动点,连接
上的两个动点,连接![]() 、
、![]() 、
、![]() ,是否存在点
,是否存在点![]() 、
、![]() ,使得
,使得![]() 是以点
是以点![]() 为直角顶点的等腰直角三角形,若存在,求点
为直角顶点的等腰直角三角形,若存在,求点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
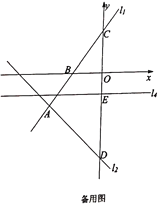
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() (a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣
(a≠0)与x轴交于A(﹣1,0)、B(﹣3,0)两点,与y轴交于点C(0,﹣3),其顶点为点D,点E的坐标为(0,﹣![]() ),该抛物线与BE交于另一点F,连接BC.
),该抛物线与BE交于另一点F,连接BC.
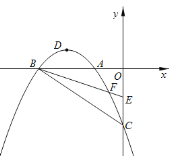
(1)求该抛物线的解析式,并用配方法把解析式化为![]() 的形式;
的形式;
(2)动点M从点D出发,沿抛物线对称轴方向向上以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com