
科目: 来源: 题型:
【题目】爱护环境越来越受到社会各界的重视,为了让学生了解环保知识,某中学组织全校![]() 名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分
名学生参加了“环保知识竞赛”.为了解本次竞赛成绩的分布情况,从中抽取了部分学生的成绩(满分![]() 分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
分,得分均为正整数)进行统计,得到下列的频率分布表.和频数分布直方图.
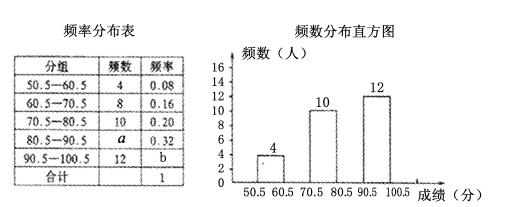
请根据以上的统计图、表解答下列问题:
(1)![]() ,
,![]() ;
;
(2)补全频数分布直方图;
(3)成绩在![]() 分以上(不含
分以上(不含![]() 分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
分)为优秀,该校所有参赛学生中成绩优秀的约为多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,点A是x轴外的一点,若平面内的点B满足:线段AB的长度与点A到x轴的距离相等,则称点B是点A的“等距点”.
(1)若点A的坐标为(0,2),点![]() (2,2),
(2,2),![]() (1,
(1,![]() ),
),![]() (
(![]() ,1)中,点A的“等距点”是_______________;
,1)中,点A的“等距点”是_______________;
(2)若点M(1,2)和点N(1,8)是点A的两个“等距点”,求点A的坐标;
(3)记函数![]() (
(![]() )的图象为
)的图象为![]() ,
,![]() 的半径为2,圆心坐标为
的半径为2,圆心坐标为![]() .若在
.若在![]() 上存在点M,
上存在点M,![]() 上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
上存在点N,满足点N是点M的“等距点”,直接写出t的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知∠MON=![]() ,P为射线OM上的点,OP=1.
,P为射线OM上的点,OP=1.
(1)如图1,![]() ,A,B均为射线ON上的点,OA=1,OB
,A,B均为射线ON上的点,OA=1,OB![]() OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.
OA,△PBC为等边三角形,且O,C两点位于直线PB的异侧,连接AC.
①依题意将图1补全;
②判断直线AC与OM的位置关系并加以证明;
(2)若![]() ,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR. 根据(1)的解答经验,直接写出△POR的面积.
,Q为射线ON上一动点(Q与O不重合),以PQ为斜边作等腰直角△PQR,使O,R两点位于直线PQ的异侧,连接OR. 根据(1)的解答经验,直接写出△POR的面积.
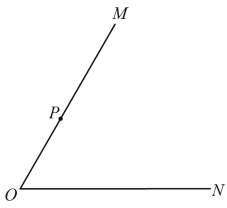
图1 备用图
查看答案和解析>>
科目: 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
科目: 来源: 题型:
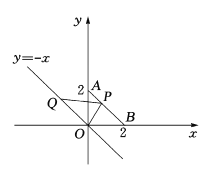
【题目】如图,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,连结
,连结![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(包括两端点),直线
上的一个动点(包括两端点),直线![]() 上有一动点
上有一动点![]() ,连结
,连结![]() ,已知
,已知![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为__________________.
的坐标为__________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】用长为6米的铝合金条制成如图所示的窗框,若窗框的高为![]() 米,窗户的透光面积为
米,窗户的透光面积为![]() 平方米(铝合金条的宽度不计).
平方米(铝合金条的宽度不计).

(1)![]() 与
与![]() 之间的函数关系式为 (不要求写自变量的取值范围);
之间的函数关系式为 (不要求写自变量的取值范围);
(2)如何安排窗框的高和宽,才能使窗户的透光面积最大?并求出此时的最大面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是小董设计的“作已知圆的内接正三角形”的尺规作图过程.
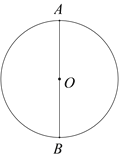
已知:⊙O.
求作:⊙O的内接正三角形.
作法:如图,
①作直径AB;
②以B为圆心,OB为半径作弧,与⊙O交于C,D两点;
③连接AC,AD,CD.
所以△ACD就是所求的三角形.
根据小董设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:在⊙O中,连接OC,OD,BC,BD,
∵OC=OB=BC,
∴△OBC为等边三角形(_______________)(填推理的依据).
∴∠BOC=60°.
∴∠AOC=180°-∠BOC=120°.
同理∠AOD=120°,
∴∠COD=∠AOC=∠AOD=120°.
∴AC=CD=AD(_______________)(填推理的依据).
∴△ACD是等边三角形.
查看答案和解析>>
科目: 来源: 题型:
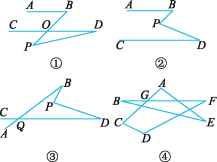
【题目】(1)如图①所示,若AB∥CD,点P在AB,CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠P+∠D,得∠P=∠B-∠D.将点P移到AB,CD内部,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD,∠B,∠D之间有何数量关系?并证明你的结论;
(2)在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图③,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?(不需证明)
(3)根据(2)的结论,求图④中∠A+∠B+∠C+∠D+∠E+∠F的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=x2+bx+c(b,c是常数)与x轴相交于A,B两点(A在B的左侧),与y轴交于点C.
(1)当A(﹣1,0),C(0,﹣3)时,求抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点.
①当点P关于原点的对称点P′落在直线BC上时,求m的值;
②当点P关于原点的对称点P′落在第一象限内,P′A2取得最小值时,求m的值及这个最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com