
科目: 来源: 题型:
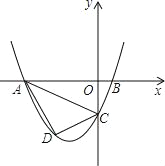
【题目】已知,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)直接写出C点的坐标;
(2)求抛物线的解析式;
(3)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料,然后解答问题:
我们新定义一种三角形,两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形.
(1)理解并填空:
①根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗? (填“是”或“不是”)
②若某三角形的三边长分别为1、![]() 、2,则该三角形 (填“是”或“不是”)奇异三角形.
、2,则该三角形 (填“是”或“不是”)奇异三角形.
(2)探究:在![]() 中,两边长分别是
中,两边长分别是![]() ,且
,且![]() ,
,![]() ,则这个三角形是否是奇异三角形?请说明理由.
,则这个三角形是否是奇异三角形?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
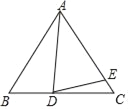
【题目】已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.
(1)如图,若点D在线段BC上,点E在线段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α= °,β= °;
②求α,β之间的关系式.
(2)请直接写出不同于以上②中的α,β之间的关系式可以是 .(写出一个即可.)
查看答案和解析>>
科目: 来源: 题型:
【题目】清明节假期,小红和小阳随爸妈去旅游,他们在景点看到一棵古松树,小红惊讶的说:“呀!这棵树真高!有60多米.”小阳却不以为然:“60多米?我看没有.”两个人争论不休,爸爸笑着说:“别争了,正好我带了一副三角板,用你们学过的知识量一量、算一算,看谁说的对吧!”
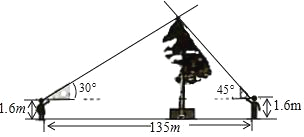
小红和小阳进行了以下测量:如图所示,小红和小阳分别在树的东西两侧同一地平线上,他们用手平托三角板,保持三角板的一条直角边与地平面平行,然后前后移动各自位置,使目光沿着三角板的斜边正好经过树的最高点,这时,测得小红和小阳之间的距离为135米,他们的眼睛到地面的距离都是1.6米.通过计算说明小红和小阳谁的说法正确(计算结果精确到0.1)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的高,
边上的高,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)联结![]() 、
、![]() ,猜想
,猜想![]() 与
与![]() 之间的关系,并写出推理过程;
之间的关系,并写出推理过程;
(3)若将锐角![]() 变为钝角
变为钝角![]() ,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
,如图(2),上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,图形中每一小格正方形的边长为1,已知△ABC
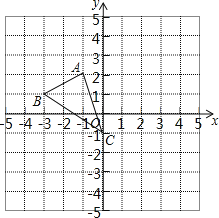
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
查看答案和解析>>
科目: 来源: 题型:
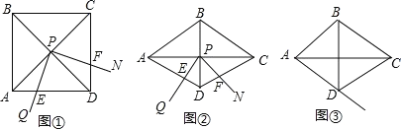
【题目】如图①,∠QPN的顶点P在正方形ABCD两条对角线交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是________;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为________,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,当点E落在线段AD的延长线上时,探究DE,DF,AD之间的数量关系(直接写出结论,不用加以证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形 OABC,以点 O 为坐标原点建立平面直角坐标系,其中 A(2,0), C(0,3),点 P 以每秒 1 个单位的速度从点 C 出发在射线 CO 上运动,连接 BP,作 BE⊥PB 交 x 轴于点 E,连接 PE 交 AB 于点 F,设运动时间为 t 秒.
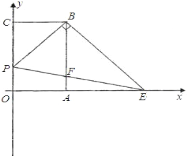
(1)当 t=2 时,求点 E 的坐标;
(2)在运动的过程中,是否存在以 P、O、E 为顶点的三角形与△PCB 相似.若存在,请求出点 P 的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
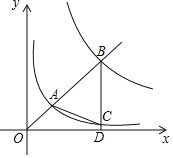
【题目】如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=![]() 和y=
和y=![]() 在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=
在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=![]() 的图象于点C,连接AC.若△ABC是等腰三角形,则k的值是_____.
的图象于点C,连接AC.若△ABC是等腰三角形,则k的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com