
科目: 来源: 题型:
【题目】双曲线![]() 与
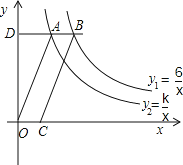
与![]() 在第一象限内的图象如图,作一条平行于x轴的直线交y1,y2于B、A,连接OA,过B作BC∥OA,交x轴于点C,若四边形OABC的面积为3,则k的值为_____.
在第一象限内的图象如图,作一条平行于x轴的直线交y1,y2于B、A,连接OA,过B作BC∥OA,交x轴于点C,若四边形OABC的面积为3,则k的值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() 是角平分线,
是角平分线,![]() .
.
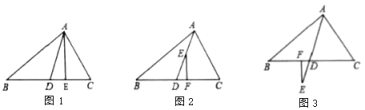
(1)如图1,![]() 是高,
是高,![]() ,
,![]() ,则
,则![]()
![]() (直接写出结论,不需写解题过程);
(直接写出结论,不需写解题过程);
(2)如图2,点![]() 在
在![]() 上,
上,![]() 于
于![]() ,试探究
,试探究![]() 与
与![]() 、
、![]() 之间的数量关系,写出你的探究结论并证明;
之间的数量关系,写出你的探究结论并证明;
(3)如图3,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于
于![]() ,则
,则![]() 与
与![]() 、
、![]() 之间的数量关系是 (直接写出结论,不需证明).
之间的数量关系是 (直接写出结论,不需证明).
查看答案和解析>>
科目: 来源: 题型:
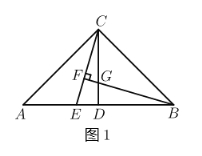
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点,直线
边上一点,直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)如图2,直线![]() 垂直于直线
垂直于直线![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目: 来源: 题型:
【题目】(1)解方程:![]() ;
;
(2)列分式方程解应用题:
用电脑程序控制小型赛车进行![]() 比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差
比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差![]() .从赛后数据得知两车的平均速度相差
.从赛后数据得知两车的平均速度相差![]() .求“畅想号”的平均速度.
.求“畅想号”的平均速度.
查看答案和解析>>
科目: 来源: 题型:
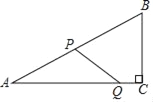
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=8,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒8个单位长度的速度运动,在BC上以每秒2个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动,两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长;(用含t的代数式表示)
(2)当点P在AB边上运动时,求PQ与△ABC的一边垂直时t的值;
(3)设△APQ的面积为S,求S与t的函数关系式;
(4)当△APQ是以PQ为腰的等腰三角形时,直接写出t的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某手机公司接到生产![]() 万部手机的订单,为尽快交货.…,求每月实际生产手机多少万部?在这道题目中,若设每月实际生产手机
万部手机的订单,为尽快交货.…,求每月实际生产手机多少万部?在这道题目中,若设每月实际生产手机![]() 万部,可得方程
万部,可得方程![]() ,则题目中“…”处省略的条件应是( )
,则题目中“…”处省略的条件应是( )
A.实际每月生产能力比原计划提高了![]() ,结果延期
,结果延期![]() 个月完成
个月完成
B.实际每月生产能力比原计划提高了![]() ,结果提前
,结果提前![]() 个月完成
个月完成
C.实际每月生产能力比原计划降低了![]() ,结果延期
,结果延期![]() 个月完成
个月完成
D.实际每月生产能力比原计划降低了![]() ,结果提前
,结果提前![]() 个月完成
个月完成
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.
(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;
(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;
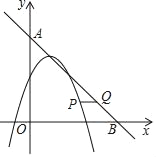
(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为![]() 时n的值.
时n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
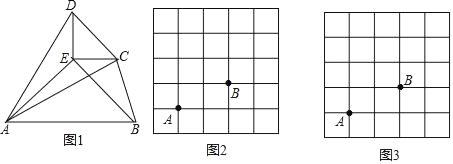
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图2,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图1,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.
查看答案和解析>>
科目: 来源: 题型:
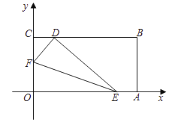
【题目】如图,将一长方形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 向终点
向终点![]() 运动,运动
运动,运动![]() 秒时,动点
秒时,动点![]() 从点
从点![]() 出发以相同的速度沿
出发以相同的速度沿![]() 向终点
向终点![]() 运动,当点
运动,当点![]() 、
、![]() 其中一点到达终点时,另一点也停止运动.
其中一点到达终点时,另一点也停止运动.
设点![]() 的运动时间为
的运动时间为![]() :(秒)
:(秒)
(1)![]() _________,
_________,![]() ___________(用含
___________(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,求点
处,求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的任意一点,过点
上的任意一点,过点![]() 作直线
作直线![]() 的平行线,与
的平行线,与![]() 轴交于
轴交于![]() 点,设直线
点,设直线![]() 的解析式为
的解析式为![]() ,当点
,当点![]() 与点
与点![]() 不重合时,设
不重合时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com