
科目: 来源: 题型:
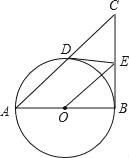
【题目】如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D作⊙O的切线交BC于点E,连接OE
(1)证明OE∥AD;
(2)①当∠BAC= °时,四边形ODEB是正方形.
②当∠BAC= °时,AD=3DE.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,AB是⊙O的直径,AB=10, ![]() ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=![]() ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.
∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.

查看答案和解析>>
科目: 来源: 题型:
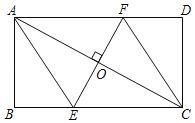
【题目】过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=6,AC=10,EC=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
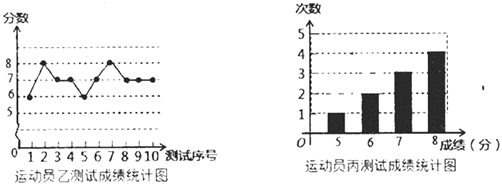
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 上一点,且
上一点,且![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,又过
,又过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,交
,交![]() 为
为![]() ,则下列说法:①
,则下列说法:①![]() 是
是![]() 的中点;②
的中点;②![]() ;③
;③![]() ;④
;④![]() 为等腰三角形;⑤连接
为等腰三角形;⑤连接![]() ,若
,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为24;其中正确的是______(填序号).
的面积为24;其中正确的是______(填序号).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD交AC于点B.若OB=4,则BC长为( )
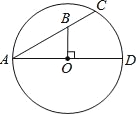
A. 2 B. 3 C. 3.6 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
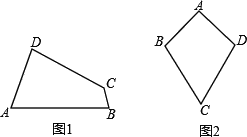
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=78°,∠B=82°,则∠C=_________,∠D=__________
(2)在探究“等对角四边形”性质时:
①小红画了一个“等对角四边形”ABCD(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
②由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例(提示:举反例可画图并说明)
(3)已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=![]() ,AD=
,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边△ABC中,点E在线段AC上,连接BE,点D在直线BC上,且CE=CD,连接ED、AD,点F是BE的中点,连接FA、FD.
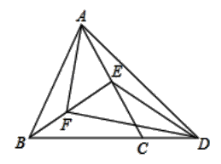
(1)若CD=6,BC=10,求△BEC的面积;
(2)当AE=CE时,求证:AD=2AF.
查看答案和解析>>
科目: 来源: 题型:
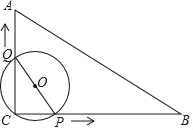
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2cm,AB=4cm,动点P从点C出发,在BC边上以每秒![]() cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒
cm的速度向点B匀速运动,同时动点Q也从点C出发,沿C→A→B以每秒4cm的速度匀速运动,运动时间为t秒![]() ,连接PQ,以PQ为直径作⊙O.
,连接PQ,以PQ为直径作⊙O.
(1)当![]() 时,求△PCQ的面积;
时,求△PCQ的面积;
(2)设⊙O的面积为s,求s与t的函数关系式;
(3)当点Q在AB上运动时,⊙O与Rt△ABC的一边相切,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com