练习册

  • 练习册
  • 试题
    相关习题
     0  358998  359006  359012  359016  359022  359024  359028  359034  359036  359042  359048  359052  359054  359058  359064  359066  359072  359076  359078  359082  359084  359088  359090  359092  359093  359094  359096  359097  359098  359100  359102  359106  359108  359112  359114  359118  359124  359126  359132  359136  359138  359142  359148  359154  359156  359162  359166  359168  359174  359178  359184  359192  366461 

    科目： 来源： 题型：

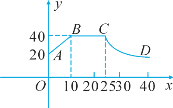
    【题目】心理学家研究发现，一般情况下，在一节40分钟的课中，学生的注意力指数y随时间x（分）的变化规律如图所示（其中AB、BC为线段,CD为双曲线的一部分）.

    （1）分别求出线段AB和双曲线CD的函数解析式，并写出自变量的取值范围；

    （2）开始上课后第5分钟时与第30分钟时比较，何时学生的注意力更集中？

    （3）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指数至少为36，那么经过适当安排，老师能否在学生达到所需的状态下讲解完这道题目？说明理由.

    查看答案和解析>>

    科目： 来源： 题型：

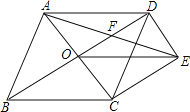
    【题目】如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且DE＝AC，连接CE、OE，连接AE交OD于点F．

    （1）求证：OE＝CD；

    （2）若菱形ABCD的边长为8，∠ABC＝60°，求AE的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某单位为了响应政府发出的“全民健身”的号召，打算在长和宽分别为20m和16m的矩形大厅内修建一个40m2的矩形健身房ABCD，该健身房的四面墙壁中有两面沿用大厅的旧墙壁(如图为平面示意图)，且每面旧墙壁上所沿用的旧墙壁长度不得超过其长度的一半，已知装修旧墙壁的费用为20元/m2，新建(含装修)墙壁的费用为80元/m2，设健身房高3m，健身房AB的长为xm，BC的长为ym，修建健身房墙壁的总投资为w元．

    （1）求y与x的函数关系式，并写出自变量x的取值范围．

    （2）求w与x的函数关系式，并求出当所建健身房AB长为8m时总投资为多少元？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（﹣2，0），与反比例函数在第一象限内的图象的交于点B（2，n），连接BO，若S△AOB=4．

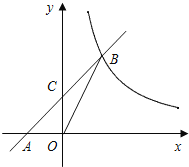
    （1）求该反比例函数的解析式和直线AB的解析式；

    （2）若直线AB与y轴的交点为C，求△OCB的面积．

    查看答案和解析>>

    科目： 来源： 题型：

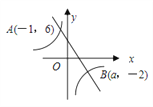
    【题目】（8分）如图，一次函数y1＝kx＋b（k≠0）和反比例函数y2＝（m≠0）的图像交于点A（－1，6）、B（a，－2）．

    （1）求一次函数与反比例函数的解析式；

    （2）根据图像直接写出y1＞y2时，x的取值范围．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在菱形ABCD中，对角线AC，BD交于点O，DE⊥AB于点E，连接OE，若DE＝，BE＝1，则∠AOE的度数是（　　）

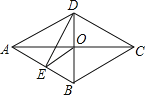
    A.30°B.45°C.60°D.75°

    查看答案和解析>>

    科目： 来源： 题型：

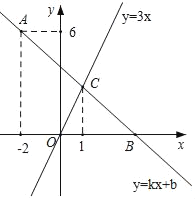
    【题目】如图，在平面直角坐标系中，一次函数y＝kx+b的图象经过点A（﹣2，6），且与x轴相交于点B，与正比例函数y＝3x的图象相交于点C，点C的横坐标为1．

    （1）求k、b的值；

    （2）请直接写出不等式kx+b﹣3x＞0的解集．

    （3）若点D在y轴上，且满足S△BCD＝2S△BOC，求点D的坐标．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某工厂计划生产甲、乙两种产品共2500吨，每生产1吨甲产品可获得利润0.3万元，每生产1吨乙产品可获得利润0.4万元．设该工厂生产了甲产品x（吨），生产甲、乙两种产品获得的总利润为y（万元）．

    （1）求y与x之间的函数表达式；

    （2）若每生产1吨甲产品需要A原料0.25吨，每生产1吨乙产品需要A原料0.5吨．受市场影响，该厂能获得的A原料至多为1000吨，其它原料充足．求出该工厂生产甲、乙两种产品各为多少吨时，能获得最大利润．

    查看答案和解析>>

    科目： 来源： 题型：

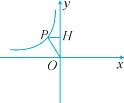
    【题目】如图是反比例函数y=的图象的一支．

    (1)求m的取值范围，并在图中画出另一支的图象；

    (2)若m＝－1，P(a，3)是双曲线上的一点，PH⊥y轴于H，将线段OP向右平移3PH的长度至O′P′，此时P的对应点P′恰好在另一条双曲线y=的图象上，则平移中线段OP扫过的面积为 ，k= .

    查看答案和解析>>

    科目： 来源： 题型：

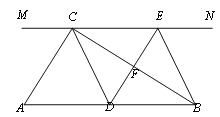
    【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．

    （1）求证：CE＝AD；

    （2）当D在AB中点时．

    ①求证：四边形BECD是菱形；
    ②当∠A为多少度时，四边形BECD是正方形？说明理由．

    查看答案和解析>>

    同步练习册答案