
科目: 来源: 题型:
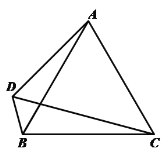
【题目】如图,在等边△![]() 中,作
中,作![]() ,边CD、BD交于点D,连接AD.
,边CD、BD交于点D,连接AD.
(1)请直接写出![]() 的度数;
的度数;
(2)求![]() 的度数;
的度数;
(3)用等式表示线段AC、BD、CD三者之间的数量关系,并证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() 和
和![]() .
.
(1)求抛物线的表达式和顶点坐标;
(2)将抛物线在A、B之间的部分记为图象M(含A、B两点).将图象M沿![]() 轴翻折,得到图象N.如果过点
轴翻折,得到图象N.如果过点![]() 和
和![]() 的直线与图象M、图象N都相交,且只有两个交点,求b的取值范围.
的直线与图象M、图象N都相交,且只有两个交点,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
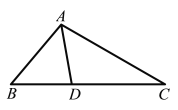
【题目】从三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的优美线.
(1)如图,在△ABC中,AD为角平分线,∠B=50°,∠C=30°,求证:AD为△ABC的优美线;
(2)在△ABC中,∠B=46°,AD是△ABC的优美线,且△ABD是以AB为腰的等腰三角形,求∠BAC的度数.
查看答案和解析>>
科目: 来源: 题型:
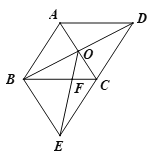
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,∠ABC=60°,过点B作AC的平行线交DC的延长线于点E.
(1) 求证:四边形ABEC为菱形;
(2) 若AB=6,连接OE,求OE的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线L1、L2、L3,若L1与L2的距离为5,L2与L3的距离7,则正方形ABCD的面积等于( )
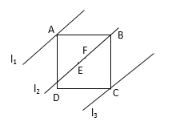
A.70B.74C.144D.148
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线![]() 与函数
与函数![]() 的图象的两个交点分别为A(a,1)、B.
的图象的两个交点分别为A(a,1)、B.
(1)求![]() ,a的值及点B的坐标;
,a的值及点B的坐标;
(2)过点P(n,0)作x轴的垂线,与直线![]() 和函数
和函数![]() 的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
的图象分别交于点M,N,当点M在点N上方时,写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习轴对称的时候,老师让同学们思考课本中的探究题.
如图(1),要在燃气管道l上修建一个泵站,分别向A、B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?
你可以在l上找几个点试一试,能发现什么规律?你可以在![]() 上找几个点试一试,能发现什么规律?
上找几个点试一试,能发现什么规律?
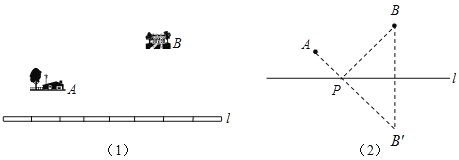
聪明的小华通过独立思考,很快得出了解决这个问题的正确办法.他把管道l看成一条直线(图(2)),问题就转化为,要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:
①作点B关于直线l的对称点B′.
②连接AB′交直线l于点P,则点P为所求.
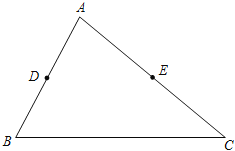
请你参考小华的做法解决下列问题.如图在△ABC中,点D、E分别是AB、AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE得周长最小.
(1)在图中作出点P(保留作图痕迹,不写作法).
(2)请直接写出△PDE周长的最小值:
.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于自变量x的不同的取值范围,有着不同的对应关系,这样的函数通常叫做分段函数.它是一个函数,而不是几个函数. 分段函数在自变量x的不同的取值范围内,函数的表达式也不同.例如:![]() 是分段函数.
是分段函数.
当![]() 时,它是二次函数
时,它是二次函数![]() ;当
;当![]() 时,它是正比例函数
时,它是正比例函数![]() .
.
(1)请在平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)求出y轴左侧图象的最低点的坐标;
(3)当![]() 时,求自变量x的值.
时,求自变量x的值.
查看答案和解析>>
科目: 来源: 题型:
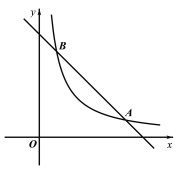
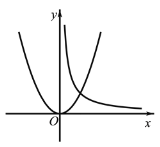
【题目】在同一直角坐标系xOy中,二次函数![]() 与反比例函数
与反比例函数![]() 的图象如图所示,如果两个函数图象上有三个不同的点A(
的图象如图所示,如果两个函数图象上有三个不同的点A(![]() ,m),B(
,m),B(![]() ,m),C(
,m),C(![]() ,m),其中m为常数,令
,m),其中m为常数,令![]() ,那么
,那么![]() 的值为___________(用含m的代数式表示).
的值为___________(用含m的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】猜想与证明:小强想证明下面的问题:“有两个角(图中的![]() 和
和![]() )相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的
)相等的三角形是等腰三角形”.但他不小心将图弄脏了,只能看见图中的![]() 和边
和边![]() .
.
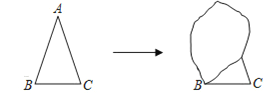
(1)请问:他能够把图恢复成原来的样子吗?若能,请你帮他写出至少两种以上恢复的方法并在备用图上恢复原来的样子.

(2)你能够证明这样的三角形是等腰三角形吗?(至少用两种方法证明)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com