
科目: 来源: 题型:
【题目】我们知道定理“直角三角形斜边上的中线等于斜边的一半”,这个定理的逆命题也是真命题.
(1)请你写出这个定理的逆命题是________;
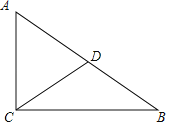
(2)下面我们来证明这个逆命题:如图,CD是△ABC的中线,CD=![]() AB.求证:△ABC为直角三角形.请你写出证明过程.
AB.求证:△ABC为直角三角形.请你写出证明过程.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲从商贩A处购买了若干斤西瓜,又从商贩B处购买了若干斤西瓜.A、B两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A、B两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )
A. 商贩A的单价大于商贩B的单价
B. 商贩A的单价等于商贩B的单价
C. 商版A的单价小于商贩B的单价
D. 赔钱与商贩A、商贩B的单价无关
查看答案和解析>>
科目: 来源: 题型:
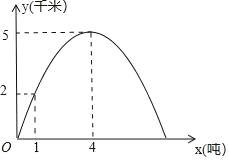
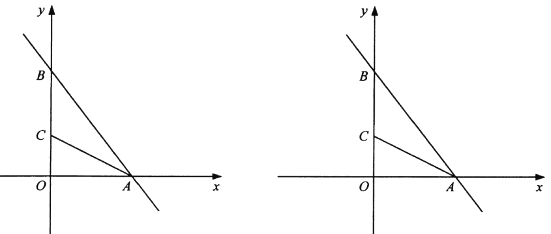
【题目】根据对宁波市相关的市场物价调研,某批发市场内甲种水果的销售利润y1(千元)与进货量x(吨)近似满足函数关系y1=0.25x,乙种水果的销售利润y2(千元)与进货量x(吨)之间的函数y2=ax2+bx+c的图象如图所示.
(1)求出y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种水果共8吨,设乙水果的进货量为t吨,写出这两种水果所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图:点E、F为线段BD的两个三等分点,四边形AECF是菱形,且菱形AECF的周长为20,BD为24,则四边形ABCD的面积为( )
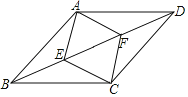
A.24B.36C.72D.144
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
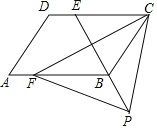
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,函数 ![]() 的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分
的图像分别与 x轴、 y轴交于 A、 B两点,点 C在 y轴上, AC平分 ![]() .
.
(1) 求点 A、 B的坐标;
(2) 求 ![]() 的面积;
的面积;
(3) 点 P在坐标平面内,且以A、 B、P为顶点的三角形是等腰直角三角形,请你直接写出点 P的坐标.
查看答案和解析>>
科目: 来源: 题型:
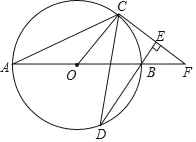
【题目】如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,OC平分∠ACD,过点C作CE⊥DB,垂足为E,直线AB与直线CE相交于F点.
(1)求证:CF为⊙O的切线;
(2)当BF=2,∠F=30°时,求BD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在A、B两地之间有汽车站C,客车由A地驶往C站,货车由B地驶往A地,两车同时出发,匀速行驶,图②是客车、货车离 C站的路程![]() 、
、![]() (km)与行驶时间x(h)之间的函数图像.
(km)与行驶时间x(h)之间的函数图像.

(1)客车的速度是 km/h;
(2)求货车由 B地行驶至 A地所用的时间;
(3)求点E的坐标,并解释点 E的实际意义.
查看答案和解析>>
科目: 来源: 题型:
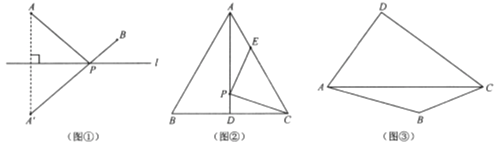
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
查看答案和解析>>
科目: 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com