
科目: 来源: 题型:
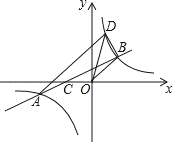
【题目】如图,点A和点B分别是反比例函数y=![]() (k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=
(k≠0)图象上两点,连接AB交x轴负半轴于点C,连接BO,tan∠BCO=![]() ,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=
,∠BOC=135°,CO=2,过点A作AD∥BO交反比例函数y=![]() 于点D,连接OD,BD.
于点D,连接OD,BD.
(1)求点A的坐标;
(2)求△OBD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A是双曲线y=![]() 上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为
上一点,过A作AB∥x轴,交直线y=﹣x于点B,点D是x轴上一点,连接BD交双曲线于点C,连接AD,若BC:CD=3:2,△ABD的面积为![]() ,tan∠ABD=
,tan∠ABD=![]() ,则k的值为( )
,则k的值为( )

A. ﹣2 B. ﹣3 C. ﹣![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】教材中这样写道“我们把多项式![]() 及
及![]() 这样的式子叫做完全平方式”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一种重要的解决数学问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决些与非负数有关的问题或求式子的最大值、最小值等.
这样的式子叫做完全平方式”如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法配方法是一种重要的解决数学问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决些与非负数有关的问题或求式子的最大值、最小值等.
例1.分解因式解:![]()
解:![]()
例2.求式子![]() 的最小值,
的最小值,
解:![]() ,
,
可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,
,
根据以上材料用配方法解决下列问题:
![]() 在实数范围内分解因式:
在实数范围内分解因式:![]() ;
;
![]() 当
当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值?并求出这个最小值.
有最小值?并求出这个最小值.
查看答案和解析>>
科目: 来源: 题型:
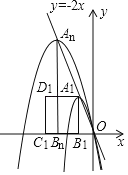
【题目】我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
(1)当抛物线经过点(﹣2,0)和(﹣1,3)时,求抛物线的表达式;
(2)当抛物线的顶点在直线y=﹣2x上时,求b的值;
(3)如图,现有一组这样的抛物线,它们的顶点A1、A2、…,An在直线y=﹣2x上,横坐标依次为﹣1,﹣2,﹣3,…,﹣n(n为正整数,且n≤12),分别过每个顶点作x轴的垂线,垂足记为B1、B2,…,Bn,以线段AnBn为边向左作正方形AnBnCnDn,如果这组抛物线中的某一条经过点Dn,求此时满足条件的正方形AnBnCnDn的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业投资112万元引进一条农产品加工生产线,若不计维修、保养等费用,预计投产后每年可创利33万元,该生产线投产后从第一年到第x年的维修、保养费用累计为y万元,且y=ax 2 +bx,若第一年的维修保养费用为2万元,第二年为4万元.
(1)求y关于x的解析式;
(2)设x年后企业纯利润为z万元(纯利润=创利-维修、保养费用),投产后这个企业在第几年就能收回投资?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com