
科目: 来源: 题型:
【题目】阅读材料,解答下列问题.
如图1,已知△ABC中,AD 为中线.延长AD至点E,使 DE=AD.在△ADC和△EDB中,AD=DE,∠ADC=∠EDB,BD=CD,所以,△ACD≌△EBD,进一步可得到AC=BE,AC//BE等结论.
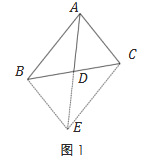
在已知三角形的中线时,我们经常用“倍长中线”的辅助线来构造全等三角形,并进一步解决一些相关的计算或证明题.
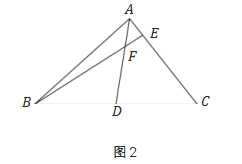
解决问题:如图2,在△ABC中,AD是三角形的中线,点F为AD上一点,且BF=AC,连结并延长BF交AC于点E,求证:AE=EF.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目: 来源: 题型:
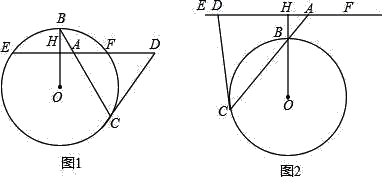
【题目】如图1,A为⊙O的弦EF上的一点,OB是和这条弦垂直的半径,垂足为H,BA的延长线交⊙O于点C,过点C作⊙O的切线与EF的延长线相交于点D.
(1)求证:DA=DC;
(2)当DF:EF=1:8,且DF=![]() 时,求ABAC的值;
时,求ABAC的值;
(3)将图1中的EF所在直线往上平行移动到⊙O外,如图2的位置,使EF与OB,延长线垂直,垂足为H,A为EF上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C,过C作⊙O的切线交EF于D.试猜想DA=DC是否仍然成立?并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是由6个大小相同的小正方形组成的方格.
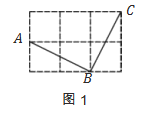
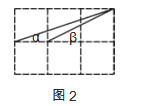
(1)如图1,A、B、C是三个格点,判断AB与BC的位置关系,并说明理由;
(2)如图2,直接写出∠α+∠β的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.
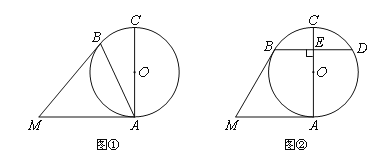
(Ⅰ)如图①,若∠BAC=250,求∠AMB的大小;
(Ⅱ)如图②,过点B作BD⊥AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.
查看答案和解析>>
科目: 来源: 题型:
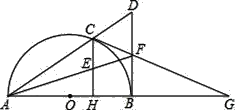
【题目】如图,已知:C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(1)求证:点F是BD中点;
(2)求证:CG是⊙O的切线;
(3)若FB=FE=2,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
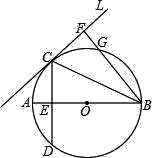
【题目】如图,已知AB是⊙O的直径,直线l与⊙O相切于点C且![]() ,弦CD交AB于E,BF⊥l,垂足为F,BF交⊙O于G.
,弦CD交AB于E,BF⊥l,垂足为F,BF交⊙O于G.
(1)求证:CE2=FGFB;
(2)若tan∠CBF=![]() ,AE=3,求⊙O的直径.
,AE=3,求⊙O的直径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC内接于⊙O,且∠B= 60°.过点C作圆的切线l与直径AD的延长线交于点E,AF⊥l,垂足为F,CG⊥AD,垂足为G.
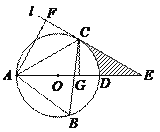
(1)求证:△ACF≌△ACG;
(2)若AF= 4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】“十九大”报告提出“实施健康中国战略”,其中雾霾天气成为环保和健康问题的焦点,为了调查学生对雾霾天气知识的了解程度,某中学在全校学生中抽取部分同学做了一次调查,根据调查结果,绘制了如下不完整的统计图表.
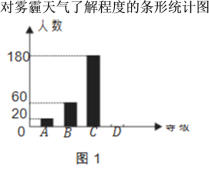
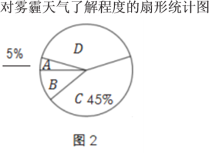
对雾霾天气了解程度的统计表
对雾霾天气知识 | 百分比 |
A. 非常了解 | 5% |
B. 比较了解 | m |
C. 基本了解 | 45% |
D. 不了解 | n |
请结合统计图表,回答下列问题:
(1)统计表中:m=__________,n=__________;
(2)请补全图1中的条形统计图;
(3)在图2所示的扇形统计图中,求D所在扇形对应的圆心角是多少度?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是一个长方体,它的长、宽、高分别为![]() 、
、![]() 、
、![]() .
.![]() 和
和![]() 是这个长方体上两个相对的顶点,点
是这个长方体上两个相对的顶点,点![]() 处有一只蚂蚁,想到点
处有一只蚂蚁,想到点![]() 处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点
处去吃可口的食物,则蚂蚁沿着长方体表面爬行到点![]() 的最短路程为__________
的最短路程为__________![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com