
科目: 来源: 题型:
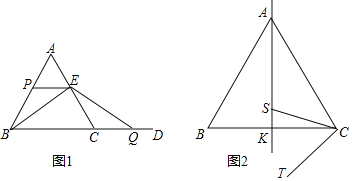
【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
(1)如图1,点![]() 在线段
在线段![]() 上从点
上从点![]() 出发沿射线
出发沿射线![]() 以
以![]() 的速度运动,过点
的速度运动,过点![]() 作
作![]() 交线段
交线段![]() 于点
于点![]() ,同时点
,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 的延长线以
的延长线以![]() 的速度运动,连接
的速度运动,连接![]() 、
、![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
①求证:![]() 是等边三角形;
是等边三角形;
②当点![]() 不与点
不与点![]() 、
、![]() 重合时,求证:
重合时,求证:![]() .
.
(2)如图2,点![]() 为
为![]() 的中点,作直线
的中点,作直线![]() ,点
,点![]() 为直线
为直线![]() 上一点,连接
上一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,则点
,则点![]() 在直线
在直线![]() 上运动的过程中,
上运动的过程中,![]() 的最小值是多少?请说明理由.
的最小值是多少?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AD=1,AB>1,AG平分∠BAD,分别过点B,C作BE⊥AG 于点E,CF⊥AG于点F,则AE-GF的值为( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(知识背景)我国古代把直角三角形较短的直角边称为“勾”,较长的的直角边称为“股”,斜边称为“弦”.据《周髀算经》记载,公元前1000多年就发现了“勾三股四弦五”的结论.像3、4、5这样为三边长能构成直角三角形的3个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;![]()
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,
当勾为3时,股![]() ,弦
,弦![]() ;
;
当勾为5时,股![]() ,弦
,弦![]() ;
;
当勾为7时,股![]() ,弦
,弦![]() .
.
请仿照上面三组样例,用发现的规律填空:
(1)如果勾用![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股
的式子表示股和弦,则股![]() ,弦
,弦![]() .
.
(问题解决)
(2)古希腊的哲学家柏拉图也提出了构造勾股数组的公式.具体表述如下:如果![]() ,
,![]() ,
,![]() 为大于1的整数),则
为大于1的整数),则![]() 、
、![]() 、
、![]() 为勾股数.请你证明柏拉图公式的正确性;
为勾股数.请你证明柏拉图公式的正确性;
(3)毕达哥拉斯在他找到的勾股数的表达式中发现弦与股的差为1,若用![]() 为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
查看答案和解析>>
科目: 来源: 题型:
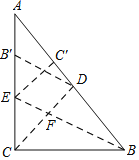
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折叠,使点B落在CA边上的B′处,展开后,再沿BE折叠,使点C落在BA边上的C′处,CD与BE交于点F.
(1)求AC′的长度;
(2)求CE的长度;
(3)比较四边形EC′DF与△BCF面积的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)在等腰三角形ABC,∠A=130°,求∠B的度数
(2)在等腰三角形ABC中,∠A=40°,求∠B的度数.
(3)根据(1)(2)问后发现,∠A的度数不同,得到∠B的度数的个数也可能不同,如果在等腰三角形ABC中,设∠A=x°,当∠B有三个不同的度数时,请你探索x的取值范围,并用含x的式子表示∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
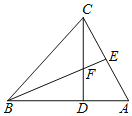
【题目】如图,在△CBD中,CD=BD,CD⊥BD,BE平分∠CBA交CD于点F,CE⊥BE垂足是E,CE的延长线与BD交于点A.
(1)求证:BF=AC;
(2)求证:BE是AC的中垂线;
(3)若BD=2,求DF的长.
查看答案和解析>>
科目: 来源: 题型:
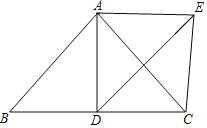
【题目】如图,在△ABC中,AB=AC,AD是中线,且AC是DE的中垂线.
(1)求证:∠BAD=∠CAD;
(2)连接CE,写出BD和CE的数量关系.并说明理由;
(3)当∠BAC=90°,BC=8时,在AD上找一点P,使得点P到点C与到点E的距离之和最小,并求出此时△BCP的面积.
查看答案和解析>>
科目: 来源: 题型:
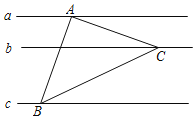
【题目】在同一平面内,有相互平行的三条直线a,b,c,且a,b之间的距离为1,b,c之间的距离是2,若等腰Rt△ABC的三个顶点恰好各在这三条平行直线上,如图所示,则△ABC的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com