
科目: 来源: 题型:
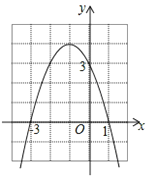
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目: 来源: 题型:
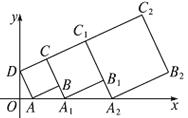
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,3).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…,按这样的规律进行下去,第2017个正方形的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
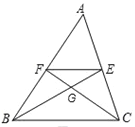
【题目】如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论:
①![]() =
=![]() ; ②
; ②![]() =
=![]() ; ③
; ③![]() =
=![]() ; ④
; ④![]() =
=![]() .其中正确的个数有( )
.其中正确的个数有( )
A. 1个 B. C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
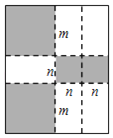
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为 ;
(2)若每块小矩形的面积为10cm2,两个大正方形和两个小正方形的面积和为58cm2,试求m+n的值
(3)②图中所有裁剪线(虚线部分)长之和为 cm.(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】我县为积极响应创建“省级卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等,从中随机抽取了部分学生成绩进行统计,绘制成如下图所示的两幅不完整的统计图表,根据图表中的信息,以下说法不正确的是( )
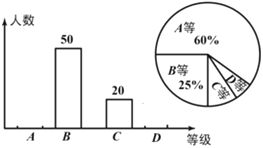
A. 样本容量是200 B. 样本中C等所占百分比是10%
C. D等所在扇形的圆心角为15° D. 估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目: 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.

查看答案和解析>>
科目: 来源: 题型:
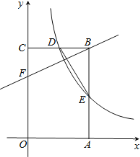
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,双曲线
,双曲线![]() ,的图象经过
,的图象经过![]() 上的点
上的点![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若若
,若若![]() 是
是![]() 的中点﹒
的中点﹒
(1)求![]() 点的坐标;
点的坐标;
(2)点![]() 是
是![]() 边上一点,若
边上一点,若![]() 和
和![]() 相似,求
相似,求![]() 的解析式;
的解析式;
(3)若点![]() 也在此反比例函数的图象上(其中
也在此反比例函数的图象上(其中![]() ),过
),过![]() 点作
点作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,若线段
,若线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 的面积是
的面积是![]() ,设
,设![]() 点的纵坐标为
点的纵坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了推动“龙江经济带”建设,我省某蔬菜企业决定通过加大种植面积、增加种植种类,促进经济发展,2017年春,预计种植西红柿、马铃薯、青椒共100公顷(三种蔬菜的种植面积均为整数),青椒的种植面积是西红柿种植面积的2倍,经预算,种植西红柿的利润可达1万元/公顷,青椒1.5万元/公顷,马铃薯2万元/公顷,设种植西红柿x公顷,总利润为y万元.
(1)求总利润y(万元)与种植西红柿的面积x(公顷)之间的关系式.
(2)若预计总利润不低于180万元,西红柿的种植面积不低于8公顷,有多少种种植方案?
(3)在(2)的前提下,该企业决定投资不超过获得最大利润的![]() 在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
在冬季同时建造A、B两种类型的温室大棚,开辟新的经济增长点,经测算,投资A种类型的大棚5万元/个,B种类型的大棚8万元/个,请直接写出有哪几种建造方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com