
科目: 来源: 题型:
【题目】综合与实践
问题情境
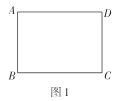
综合与实践课上,老师让同学们以“折纸”为主题开展数学活动.如图1,有一张长为4,宽为3的矩形纸片![]() (
(![]() ).
).
操作发现
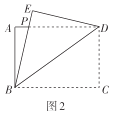
(1)快乐小组先将图1中的矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在点
落在点![]() 处,得到图2,他们发现
处,得到图2,他们发现![]() ,请你证明这个结论;
,请你证明这个结论;
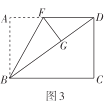
(2)创新小组将图2中的矩形纸片展开后继续折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,得到图3,则折痕
,得到图3,则折痕![]() __________;
__________;
实践探究
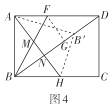
(3)前进小组在创新小组的操作基础上,将图3中的纸片展开,再将矩形纸片![]() 沿直线
沿直线![]() 折叠,使得点
折叠,使得点![]() 落在对角线
落在对角线![]() 上的点
上的点![]() 处,然后将纸片展平.如图4所示,折痕
处,然后将纸片展平.如图4所示,折痕![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
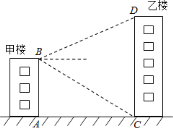
【题目】已知甲楼高![]() 米,自甲楼楼顶
米,自甲楼楼顶![]() 处看乙楼楼顶
处看乙楼楼顶![]() 的仰角为
的仰角为![]() ,看乙楼楼底
,看乙楼楼底![]() 的俯角为
的俯角为![]() ,现要在两楼楼顶
,现要在两楼楼顶![]() 、
、![]() 之间拉一横幅,求乙楼的高度
之间拉一横幅,求乙楼的高度![]() 以及横幅
以及横幅![]() 的长度.(结果均精确到
的长度.(结果均精确到![]() 米)
米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 是等边三角形
是等边三角形![]() 内一点,连接
内一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .以
.以![]() 为顶点,
为顶点,![]() 为一边,在
为一边,在![]() 外部作
外部作![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)根据推理可得![]() __________,
__________,![]() __________;(用含
__________;(用含![]() 的代数式表示)
的代数式表示)
(3)探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目: 来源: 题型:
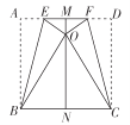
【题目】寒假丽丽用一块边长为10的正方形彩纸为她的人偶玩具做了一件披风,如图所示,先将正方形纸片![]() 对折,展平后得到中线
对折,展平后得到中线![]() ,再分别沿折痕
,再分别沿折痕![]() ,
,![]() 将点
将点![]() ,点
,点![]() 都折到
都折到![]() 上点
上点![]() 处,此时领口
处,此时领口![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目: 来源: 题型:
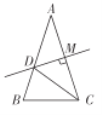
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则以下结论:①
,则以下结论:①![]() 是等腰三角形;②
是等腰三角形;②![]() 是
是![]() 的角平分线;③
的角平分线;③![]() 的周长
的周长![]() ;④
;④![]() 正确的有( )
正确的有( )
A.①②B.①③C.③④D.②④
查看答案和解析>>
科目: 来源: 题型:
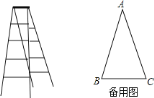
【题目】如图,是一种用于装修的人字形梯,合拢时,梯子的长为![]() 米,距调查,这种梯子在张角为
米,距调查,这种梯子在张角为![]() 时最安全.
时最安全.
(1)求梯子最安全时,梯子能达到的最大高度是多少?(精确到![]() 米)
米)
(2)装修时,房顶距离地面![]() 米,一个人坐在梯子最顶端时,他的手臂能达到的最大高度比梯子最顶端高出
米,一个人坐在梯子最顶端时,他的手臂能达到的最大高度比梯子最顶端高出![]() 米.要使装修正常进行,那么梯子张角至多为多少度?(精确到
米.要使装修正常进行,那么梯子张角至多为多少度?(精确到![]() 度)
度)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两条边对应相等的两个三角形全等
B.两腰对应相等的两个等腰三角形全等
C.两角对应相等的两个等腰三角形全等
D.一边对应相等的两个等边三角形全等
查看答案和解析>>
科目: 来源: 题型:
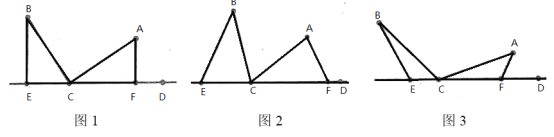
【题目】直线CD是经过∠BCA顶点C的一条直线,CA=CB,点E、F分别是直线CD上的两点,且∠BEC=∠CFA=∠BCA,
(1)如图1,当∠BCA=90时,则BE与CF的数量关系是:______________
(2)如图2,当∠BCA为锐角时,(1)中的数量关系是否依然成立?若成立,请证明
(3)如图 3,当∠BCA为钝角时,请说出EF、BE、AF三条线段的数量关系(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com