
科目: 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目: 来源: 题型:
【题目】(8分)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.

(1)求证:PB是⊙O的切线;
(2)当OB=3,PA=6时,求MB,MC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数![]() ,当其自变量的值为
,当其自变量的值为![]() 时,其函数值等于
时,其函数值等于![]() ,则称
,则称![]() 为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差
为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差![]() 称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度
称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度![]() 为零.例如,图1中的函数有0,1两个不变值,其不变长度
为零.例如,图1中的函数有0,1两个不变值,其不变长度![]() 等于1.
等于1.
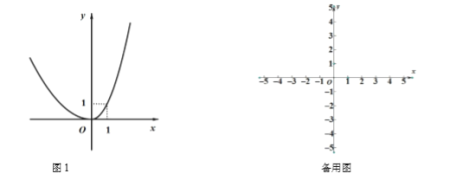
(1)分别判断函数![]() ,
,![]() 有没有不变值?如果有,请写出其不变长度;
有没有不变值?如果有,请写出其不变长度;
(2)函数![]() 且
且![]() ,求其不变长度
,求其不变长度![]() 的取值范围;
的取值范围;
(3)记函数![]() 的图像为
的图像为![]() ,将
,将![]() 沿
沿![]() 翻折后得到的函数图像记为
翻折后得到的函数图像记为![]() ,函数
,函数![]() 的图像由
的图像由![]() 和
和![]() 两部分组成,若其不变长度
两部分组成,若其不变长度![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
(3)若![]() 点在
点在![]() 点左边,在第一象限内,(2)中所得到抛物线上是否存在一点
点左边,在第一象限内,(2)中所得到抛物线上是否存在一点![]() ,使直线
,使直线![]() 分
分![]() 的面积为
的面积为![]() 两部分?若存在,求出
两部分?若存在,求出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形![]() 中,连接
中,连接![]() ,
,![]() 为射线
为射线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),连接
不重合),连接![]() ,
,![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
提出问题:当点![]() 运动时,
运动时,![]() 的度数是否发生改变?
的度数是否发生改变?
探究问题:
(1)首先考察点![]() 的两个特殊位置:
的两个特殊位置:
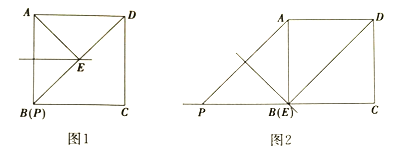
①当点![]() 与点
与点![]() 重合时,如图1所示,
重合时,如图1所示,![]() ____________
____________![]()
②当![]() 时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
(2)然后考察点![]() 的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)
的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)

(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图3和图4中任选一个进行证明;若不成立,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)计算:2﹣1+(π﹣3.14)0+sin60°﹣|﹣![]() |
|
(2)如图,在△ABC中,AB=AC=10,sinC=![]() ,点D是BC上一点,且DC=AC.求BD的长.
,点D是BC上一点,且DC=AC.求BD的长.
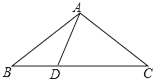
查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂计划生产甲、乙两种产品共2500吨,每生产1吨甲产品可获得利润0.3万元,每生产1吨乙产品可获得利润0.4万元.设该工厂生产了甲产品x(吨),生产甲、乙两种产品获得的总利润为y(万元).
(1)求y与x之间的函数表达式;
(2)若每生产1吨甲产品需要A原料0.25吨,每生产1吨乙产品需要A原料0.5吨.受市场影响,该厂能获得的A原料至多为1000吨,其它原料充足.求出该工厂生产甲、乙两种产品各为多少吨时,能获得最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com