
科目: 来源: 题型:
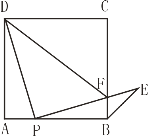
【题目】如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当![]() 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
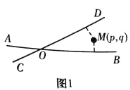
【题目】定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”为(0,0)的点有1个,即点O.
(1)“距离坐标”为1,0的点有 个;
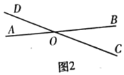
(2)如图2,若点M在过点O且与直线AB垂直的直线l上时,点M的“距离坐标”为p,q,且BOD 150,请写出p、q的关系式并证明;
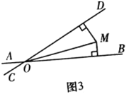
(3)如图3,点M的“距离坐标”为![]() ,且DOB 30,求OM的长.
,且DOB 30,求OM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目: 来源: 题型:
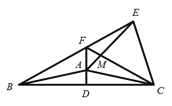
【题目】已知:如图,在等腰三角形ABC中,120BAC180,ABAC,ADBC于点D,以AC为边作等边三角形ACE,ACE与ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
(1)求EFC的度数;
(2)求证:FE+FA=FC.
查看答案和解析>>
科目: 来源: 题型:
【题目】金桔是浏阳的特色水果,金桔一上市,水果店的老板就用1200元购进一批金桔,很快售完,老板又用2500元购进第二批金桔,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批金桔每件进价为多少元?
(2)水果店老板销售这两批金桔时,每件售价都是150元,当第二批金桔售出80%后,决定打七折促销,结果全部售完,水果店老板共盈利多少元?
查看答案和解析>>
科目: 来源: 题型:
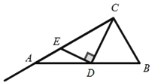
【题目】如图,在ABC中,ACB 90,BAC 30, AB2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当ADE为等腰三角形时,AD的长度为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目: 来源: 题型:
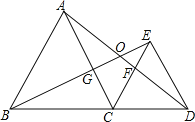
【题目】如图,△ABC和△ECD都是等边三角形,B、C、D三点在一条直线上,AD与BE相交于点O,AD与CE相交于点F,AC与BE相交于点G.
(1)△BCE与△ACD全等吗?请说明理由.
(2)求∠BOD度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,如果点![]() 、点
、点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 、
、![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 、
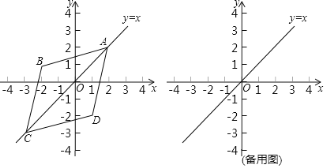
、![]() 的“极好菱形”.如图为点
的“极好菱形”.如图为点![]() 、
、![]() 的“极好菱形”的一个示意图.已知点
的“极好菱形”的一个示意图.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“极好菱形”的顶点的是 .
的“极好菱形”的顶点的是 .
(2)若点![]() 、
、![]() 的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标.
的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标.
(3)如果四边形![]() 是点
是点![]() 、
、![]() 的“极好菱形”.
的“极好菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
②当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 的直线分别交边
的直线分别交边![]() 、
、![]() 、
、![]() 、
、![]() 于点
于点![]() 、
、![]() 、
、![]() 、
、![]()
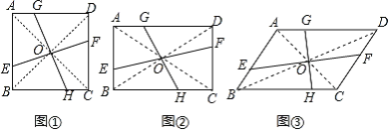
(1)如图①,若四边形![]() 是正方形,且
是正方形,且![]() ,易知
,易知![]() ,又因为
,又因为![]() ,所以
,所以![]() (不要求证明)
(不要求证明)
(2)如图②,若四边形![]() 是矩形,且
是矩形,且![]() ,若
,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长(用含
的长(用含![]() 、
、![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)如图③,若四边形![]() 是平行四边形,且
是平行四边形,且![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com