
科目: 来源: 题型:
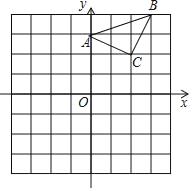
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】(2014浙江金华)如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=3,另两边与反比例函数![]() (k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
(k≠0)的图象分别相交于点E、F,且DE=2.过点E作EH⊥x轴于点H,过点F作FG⊥EH于点G.回答下面的问题:
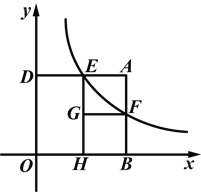
(1)①求反比例函数的解析式.
②当四边形AEGF为正方形时,求点F的坐标.
(2)小亮进一步研究四边形AEGF的特征后提出问题:“当AE>EG时,矩形AEGF与矩形DOHE能否全等?能否相似?”
针对小亮提出的问题,请你判断这两个矩形能否全等(直接写出结论即可).这两个矩形能否相似?若能相似,求出相似比;若不能相似,试说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(8分)如图,一次函数![]() (
(![]() )的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
)的图象经过点C(3,0),且与两坐标轴围成的三角形的面积为3.
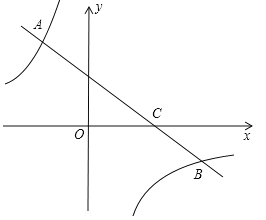
(1)求该一次函数的解析式;
(2)若反比例函数![]() 的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
的图象与该一次函数的图象交于二、四象限内的A、B两点,且AC=2BC,求m的值.
查看答案和解析>>
科目: 来源: 题型:
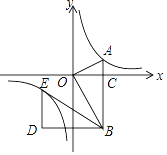
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(![]() ,1)在反比例函数y=
,1)在反比例函数y=![]() 的图象上.
的图象上.
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.
细心观察图形,认真分析下列各式,然后解答问题:
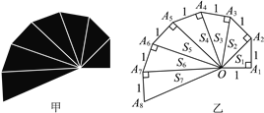
(![]() )2+1=2,S1=
)2+1=2,S1=![]() ;(
;(![]() )2+1=3,S2=
)2+1=3,S2=![]() ;(
;(![]() )2+1=4,S3=
)2+1=4,S3=![]() ;….
;….
(1)请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;
(2)求出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)

(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com