
科目: 来源: 题型:
【题目】如图,一艘轮船在位于灯塔P的北偏东30°方向,距离灯塔120海里的A处.轮船沿正南方向航行一段时间后,到达位于灯塔P的南偏东64°方向上的B处.求轮船所在的B处与灯塔P的距离.(结果精确到0.1海里)(参考数据:sin64°=0.90,cos64°=0.44,tan64°=2.05)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点A在抛物线y=x2﹣2x+2上运动,过点A作AC上x轴于点C,以AC为对角线作矩形ABCD,连结BD,则BD的最小值为( )
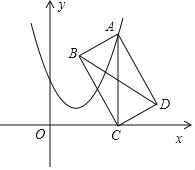
A. ![]() B. 1 C.
B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目: 来源: 题型:
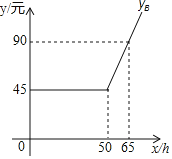
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,∠DAB=130°,连结OC,P是半径OC上的一个动点,连结PD、PB,则么DPB的大小可能为( )
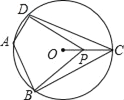
A. 40° B. 80° C. 110° D. 130°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

查看答案和解析>>
科目: 来源: 题型:
【题目】若关于x的三个方程x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m﹣1)x2+2mx+m﹣1=0中至少有一个方程有实根,则m的取值范围是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】某水库大坝的横截面是如图所示的四边形BACD,期中AB∥CD.瞭望台PC正前方水面上有两艘渔船M、N,观察员在瞭望台顶端P处观测渔船M的俯角![]() ,观测渔船N在俯角
,观测渔船N在俯角![]() ,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
,已知NM所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米);
(2)已知坝高24米,坝长100米,背水坡AD的坡度![]() .为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为
.为提高大坝防洪能力,某施工队在大坝的背水坡填筑土石方加固,加固后坝定加宽3米,背水坡FH的坡度为![]() ,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据:
,施工12天后,为尽快完成加固任务,施工队增加了机械设备,工作效率提高到原来的1.5倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?(参考数据: ![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】(9分)如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°,求大树的高度. (结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源: 题型:
【题目】假期,六盘水市教育局组织部分教师分别到A.B.C.D四个地方进行新课程培训,教育局按定额购买了前往四地的车票.如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
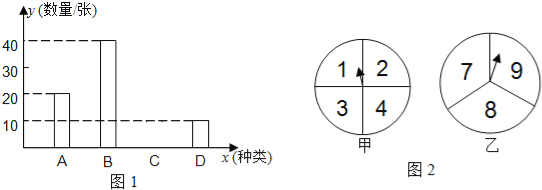
(1)若去C地的车票占全部车票的30%,则去C地的车票数量是 张,补全统计图.
(2)若教育局采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么余老师抽到去B地的概率是多少?
(3)若有一张去A地的车票,张老师和李老师都想要,决定采取旋转转盘的方式来确定.其中甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2所示.具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,票给李老师,否则票给张老师(指针指在线上重转).试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com