
科目: 来源: 题型:
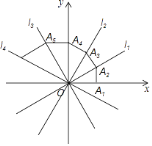
【题目】如图,四条直线l1:y1=![]() x,l2:y2=
x,l2:y2=![]() x,l3:y3=﹣
x,l3:y3=﹣![]() x,l4:y4=﹣
x,l4:y4=﹣![]() x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
x,OA1=1,过点A1作A1A2⊥x轴,交l1于点A2,再过点A2作A2A3⊥l1交l2于点A3,再过点A3作A3A4⊥l2交y轴于点A4…,则点A2017坐标为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点D、E分别是边AB、AC的中点,∠B=50°,∠A=26°,将△ABC沿DE折叠,点A的对应点是点A′,则∠AEA′的度数是( )

A. 145° B. 152° C. 158° D. 160°
查看答案和解析>>
科目: 来源: 题型:
【题目】下面一元二次方程的解法中,正确的是( )
A. (x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
B. (2-5x)+(5x-2)2=0,∴(5x-2)(5x-3)=0,∴x1=![]() ,x2=
,x2=![]()
C. (x+2)2+4x=0,∴x1=2,x2=-2
D. x2=x 两边同除以x,得x=1
查看答案和解析>>
科目: 来源: 题型:
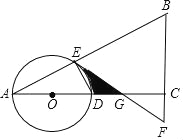
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,以OA为半径的圆分别交AB、AC于点E、D,在BC的延长线上取点F,使得BF=EF.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若∠A=30°,求证:DG=![]() DA;
DA;
(3)若∠A=30°,且图中阴影部分的面积等于2![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
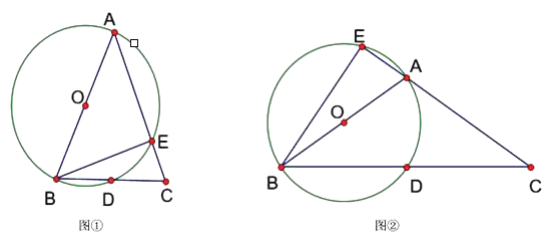
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
(1)判断直线PC与⊙O的位置关系,并说明理由.
(2)若AB=5![]() ,BC=10,求⊙O的半径及PC的长.
,BC=10,求⊙O的半径及PC的长.

查看答案和解析>>
科目: 来源: 题型:
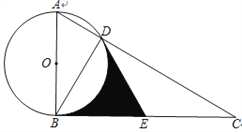
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB.
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2, 求阴影部分面积.
查看答案和解析>>
科目: 来源: 题型:
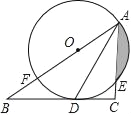
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°,
(1)请判断CD是否⊙O的切线?并说明理由;
(2)若⊙O的半径为6,求弧AC的长.(结果保留π)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com