
科目: 来源: 题型:
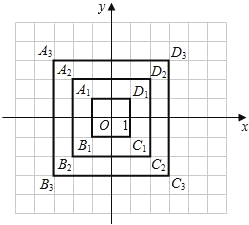
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,已知AB=BC,BG=BE,点A,B,E在同一直线上,P是线段DF的中点,连接PG,PC,若∠DCB=∠GEF=120°,则![]() =( )
=( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目: 来源: 题型:
【题目】某学习小组做“用频率估计概率的试验时,统计了某一结果出现的频率,绘制了如图所示折线统计图,则符合这一结果的试验最有可能的是( )
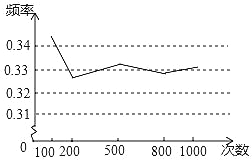
A. 掷一枚正六面体的骰子,出现1点朝上
B. 任意写一个整数,它能被2整除
C. 不透明袋中装有大小和质地都相同的1个红球和2个黄球,从中随机取一个,取到红球
D. 先后两次掷一枚质地均匀的硬币,两次都出现反面
查看答案和解析>>
科目: 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
科目: 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,AC是⊙O的直径,DE⊥AB,垂足为E.
(1)延长DE交⊙O于点F,延长DC,FB交于点P,如图1.求证:PC=PB;
(2)过点B作BG⊥AD,垂足为G,BG交DE于点H,且点O和点A都在DE的左侧,如图2.若AB=![]() ,DH=1,∠OHD=80°,求∠BDE的大小.
,DH=1,∠OHD=80°,求∠BDE的大小.
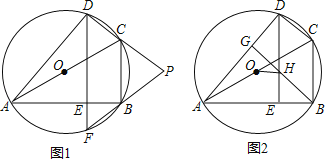
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知D,E分别为△ABC的边AB,BC上两点,点A,C,E在⊙D上,点B,D在⊙E上.F为![]() 上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
上一点,连接FE并延长交AC的延长线于点N,交AB于点M.
(1)若∠EBD为α,请将∠CAD用含α的代数式表示;
(2)若EM=MB,请说明当∠CAD为多少度时,直线EF为⊙D的切线;
(3)在(2)的条件下,若AD=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目: 来源: 题型:
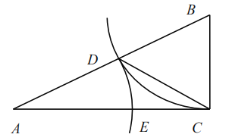
【题目】如图,在△ABC中,∠ACB=90°,以点B为圆心,BC长为半径画弧,交边AB与点D,以A为圆心,AD长为半径画弧,交边AC于点E,连接CD.
(1)若∠A=28°,求∠ACD的度数;
(2)设BC=a,AC=b.
①线段AD的长是方程![]() 的一个根吗?为什么?
的一个根吗?为什么?
②若AD=EC,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销,该店决定降价销售,经市场调查反应:每降价1元,每星期可多卖10件![]() 已知该款童装每件成本30元
已知该款童装每件成本30元![]() 设该款童装每件售价x元,每星期的销售量为y件.
设该款童装每件售价x元,每星期的销售量为y件.
![]() 求y与x之间的函数关系式
求y与x之间的函数关系式![]() 不求自变量的取值范围
不求自变量的取值范围![]() ;
;
![]() 当每件童装售价定为多少元时,该店一星期可获得3910元的利润?
当每件童装售价定为多少元时,该店一星期可获得3910元的利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com