【题目】如图，菱形的边长为，点在对角线上(点在点的左侧)，且则的最小值为____．

【题目】如图，在平面直角坐标系中，一次函数的图像分别交x、y轴于点A、B，抛物线经过点A、B，点P为第四象限内抛物线上的一个动点.

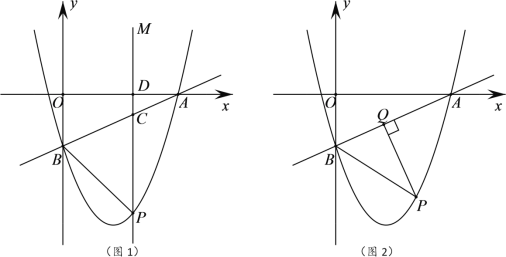
（1）求此抛物线对应的函数表达式；

（2）如图1所示，过点P作PM∥y轴，分别交直线AB、x轴于点C、D，若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似，求点P的坐标；

（3）如图2所示，过点P作PQ⊥AB于点Q，连接PB，当△PBQ中有某个角的度数等于∠OAB度数的2倍时，请直接写出点P的横坐标.

【题目】如图，为的直径，于点，是上一点，且，延长至点，连接，使，延长与交于点，连结，．

（1）连结，求证：；

（2）求证：是的切线；

（3）若，，求的值．

（1）甲、乙两种商品的销售单价各多少元？

（2）市场调研表明：所有商品能全部售出，企业要求生产乙种商品的数量不超过甲种商品数量的，且甲、乙两种商品的销售总收入不低于3300万元，请你为该企业设计一种生产方案，使销售总利润最大．

（1）求证：四边形ADCF是菱形；

（3）若AC＝6，AB＝8，求菱形ADCF的面积．

【题目】某货站传送货物的平面示意图如图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带长为．

（1）求新传送带的长度；

（2）如果需要在货物着地点的左侧留出的通道，试判断距离点处的货物是否需要挪走，并说明理由．（说明：（1），（2）的计算结果精确到，参考数据：，，，）

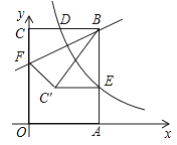
【题目】以矩形的顶点为坐标原点建立平面直角坐标系，使点、分别在、轴的正半轴上，双曲线的图象经过的中点，且与交于点，过边上一点，把沿直线翻折，使点落在矩形内部的一点处，且，若点的坐标为（2，4），则的值为______．

【题目】如图，正方形的边长为，在正方形外，，过作于，直线，交于点，直线交直线于点，则下列结论正确的是（ ）

①；②；③；

④若，则

A.1个B.2个C.3个D.4个

（1）该社区九月份购买甲、乙两种绿色植物各多少盆？

（2）十月份，该社区决定再次购买甲、两种绿色植物．已知十月份甲种绿色植物每盆的价格比九月份的价格优惠元，十月份乙种绿色植物每盆的价格比九月份的价格优惠．因创卫需要，该社区十月份购买甲种绿色植物的数量比九月份的数量增加了，十为份购买乙种绿色植物的数量比九月份的数量增加了．若该社区十月份的总花费与九月份的总花费恰好相同，求的值．

【题目】若一个三位数的百位上的数字减去十位上的数字等于其个位上的数字，则称这个三位数为“差数”，同时，如果百位上的数字为、十位上的数字为，三位数是“差数”，我们就记：，其中，，．例如三位数514．∵，∴514是“差数”，∴．

（1）已知一个三位数的百位上的数字是6，若是“差数”，，求的值；

（2）求出小于300的所有“差数”的和，若这个和为，请判断是不是“差数”，若是，请求出；若不是，请说明理由．