科目： 来源： 题型：
【题目】如图，正方形OABC的一个顶点O是平面直角坐标系的原点，顶点A，C分别在y轴和x轴上，P为边OC上的一个动点，且PQ⊥BP，PQ=BP，当点P从点C运动到点O时，可知点Q始终在某函数图象上运动，则其函数图象是（ ）
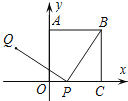
A.线段B.圆弧
C.双曲线的一部分D.抛物线的一部分
查看答案和解析>>
科目： 来源： 题型：
【题目】（2016广西贺州市）如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（ ）
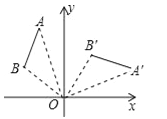
A. （2，5） B. （5，2） C. （2，﹣5） D. （5，﹣2）
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，抛物线
交x轴于点A（-3，0）和点B，交y轴于点C（0，3）．
（1）求抛物线的函数表达式；
（2）若点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，求线段DQ长度的最大值．
（3）点G是抛物线上的动点，点F在x轴上的动点，若以A，C，F，G四个点为顶点的四边形是平行四边形，求出所有满足条件的点F坐标（直接写出结果）．
查看答案和解析>>
科目： 来源： 题型：
【题目】（1）操作发现：如图①，小明画了一个等腰三角形ABC，其中AB=AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是__________；位置关系是__________．
（2）类比思考：
如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB＞AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．
（3）深入研究：
如图③，小明在（2）的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．
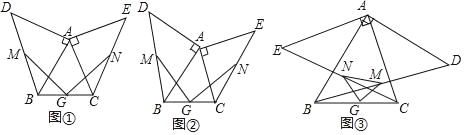
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，AD是等腰△ABC底边BC上的高，点O是AC中点，延长DO到E
使AE∥BC，连接AE。
（1）求证：四边形ADCE是矩形；
（2）①若AB=17，BC=16，则四边形ADCE的面积＝ ；
②若AB=10，则BC＝ 时，四边形ADCE是正方形。
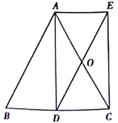
查看答案和解析>>
科目： 来源： 题型：
【题目】诗词是我国古代文化中的瑰宝，某市教育主管部门为了解本市初中生对诗词的学习情况；举了一次“中华诗词”背诵大赛，随机抽取了部分同学的成绒（
为整数，总分100分），绘制了如下尚不完整的统计图表.
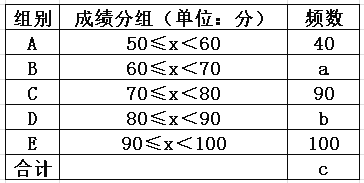
根据以上信息解答下列问题：
（1）统计表中
________，
________，
________；
（2）扇形统计图中，
的值为________，“
”所对应的圆心角的度数是________（度）；
（3）若参加本次大赛的同学共有4000人，请你估计成绩在80分及以上的学生大约有多少人？
查看答案和解析>>
科目： 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②4a+c＜2b；③3b+2c＜0；④m（am+b）+b＜a（m≠﹣1），其中正确结论的个数是（ ）
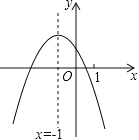
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目： 来源： 题型：
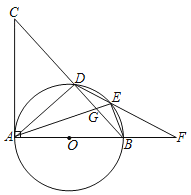
【题目】如图，AB是⊙O的直径，AC⊥AB，BC交⊙O于点D，点E在劣弧BD上，DE的延长线交AB的延长线于点F，连接AE交BD于点G．
（1）求证：∠AED＝∠CAD；
（2）若点E是劣弧BD的中点，求证：ED2＝EGEA；
（3）在（2）的条件下，若BO＝BF，DE＝2，求EF的长．
查看答案和解析>>
科目： 来源： 题型：
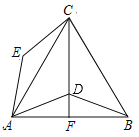
【题目】如图，点D是等边△ABC内一点，将线段AD绕着点A逆时针旋转60°得到线段AE，连结CD并延长交AB于点F，连结BD，CE．
（1）求证：△ACE≌△ABD；
（2）当CF⊥AB时，∠ADB＝140°，求∠ECD的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
