
科目: 来源: 题型:
【题目】体育李老师为了解九年级女生体质健康的变化情况,本学期从九年级全体90名女生中随机抽取15名女生进行体质测试,并调取该15名女生上学期的体质测试成绩进行对比,李老师对两次数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .两次测试成绩(百分制)的频数分布直方图如下(数据分组:
.两次测试成绩(百分制)的频数分布直方图如下(数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
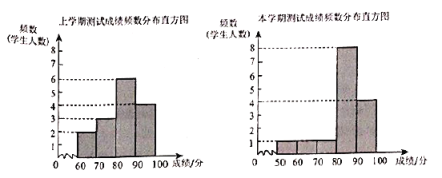
![]() .上学期测试成绩在
.上学期测试成绩在![]() 的是:80 81 83 84 84 88
的是:80 81 83 84 84 88
![]() .两个学期测试成绩的平均数、中位数、众数如下:
.两个学期测试成绩的平均数、中位数、众数如下:
学期 | 平均数 | 中位数 | 众数 |
上学期 | 82.9 |
| 84 |
本学期 | 83 | 86 | 86 |
根据以上信息,回答下列问题:
(1)表中![]() 的值是______;
的值是______;
(2)体育李老师计划根据本学期统计数据安排80分以下(不含80分)的同学参加体质加强训练项目,则九年级约有______名女生参加此项目;
(3)分析这15名女生从上学期到本学期体质健康变化的总体情况.(从两个方面进行分析)
查看答案和解析>>
科目: 来源: 题型:
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
查看答案和解析>>
科目: 来源: 题型:
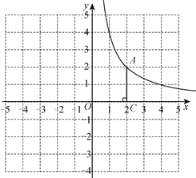
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象经过点
的图象经过点![]() ,作AC⊥x轴于点C.
,作AC⊥x轴于点C.
(1)求k的值;
(2)直线AB:![]() 图象经过点
图象经过点![]() 交x轴于点
交x轴于点![]() .横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
.横、纵坐标都是整数的点叫做整点.线段AB,AC,BC围成的区域(不含边界)为W.
①直线AB经过![]() 时,直接写出区域W内的整点个数;
时,直接写出区域W内的整点个数;
②若区域W内恰有1个整点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
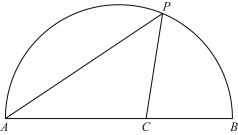
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=a![]() -4ax与x轴交于A,B两点(A在B的左侧).
-4ax与x轴交于A,B两点(A在B的左侧).
(1)求点A,B的坐标;
(2)已知点C(2,1),P(1,-![]() a),点Q在直线PC上,且Q点的横坐标为4.
a),点Q在直线PC上,且Q点的横坐标为4.
①求Q点的纵坐标(用含a的式子表示);
②若抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合)使得
可以重合)使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对平衡点.
的一对平衡点.
(1)如图1,已知点![]() ,
,![]() ;
;
①设点![]() 与线段
与线段![]() 上一点的距离为
上一点的距离为![]() ,则
,则![]() 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是线段
是线段![]() 的一对平衡点的是 ;
的一对平衡点的是 ;
(2)如图2,已知![]() 的半径为1,点
的半径为1,点![]() 的坐标为
的坐标为![]() 在第一象限,且点
在第一象限,且点![]() 与点
与点![]() 是
是![]() 的一对平衡点,求
的一对平衡点,求![]() 的取值范围;
的取值范围;
(3)如图3,已知点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 的正半轴于点
的正半轴于点![]() .点
.点![]() (其中
(其中![]() )是坐标平面内一个动点,且
)是坐标平面内一个动点,且![]() ,
,![]() 是以点
是以点![]() 为圆心,半径为2的圆,若
为圆心,半径为2的圆,若![]() 上的任意两个点都是
上的任意两个点都是![]() 的一对平衡点,直接写出
的一对平衡点,直接写出![]() 的取值范围.
的取值范围.



查看答案和解析>>
科目: 来源: 题型:
【题目】下表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
“正面向上”次数 | 22 | 52 | 68 | 101 | 116 | 147 | 160 | 187 | 214 | 238 |
“正面向上”频率 | 0.44 | 0.52 | 0.45 | 0.51 | 0.46 | 0.49 | 0.46 | 0.47 | 0.48 | 0.48 |
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是__________(填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com