
科目: 来源: 题型:
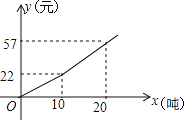
【题目】为鼓励市民节约用水,某市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系
(1)小红家五月份用水8吨,应交水费_____元;
(2)按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
科目: 来源: 题型:
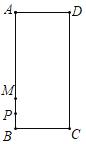
【题目】如图,矩形ABCD中,动点P沿B→A→D→C→B路线运动,点M是AB边上的一点,且MB=![]() AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
AB,已知AB=4,BC=2,AP=2MP,则点P到边AD的距离为_______.
查看答案和解析>>
科目: 来源: 题型:
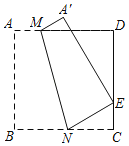
【题目】如图,把正方形纸片ABCD沿对边上的两点M、N所在的直线对折,使点B落在边CD上的点E处,折痕为MN,其中CE=![]() CD.若AB的长为2,则MN的长为( )
CD.若AB的长为2,则MN的长为( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
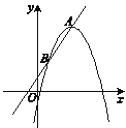
【题目】如图,在平面直角坐标系xOy中,直线![]() 和抛物线W交于A,B两点,其中点A是抛物线W的顶点.当点A在直线
和抛物线W交于A,B两点,其中点A是抛物线W的顶点.当点A在直线![]() 上运动时,抛物线W随点A作平移运动.在抛物线平移的过程中,线段AB的长度保持不变.
上运动时,抛物线W随点A作平移运动.在抛物线平移的过程中,线段AB的长度保持不变.
应用上面的结论,解决下列问题:
在平面直角坐标系xOy中,已知直线![]() .点A是直线
.点A是直线![]() 上的一个动点,且点A的横坐标为
上的一个动点,且点A的横坐标为![]() .以A为顶点的抛物线
.以A为顶点的抛物线![]() 与直线
与直线![]() 的另一个交点为点B.
的另一个交点为点B.
(1)当![]() 时,求抛物线
时,求抛物线![]() 的解析式和AB的长;
的解析式和AB的长;
(2)当点B到直线OA的距离达到最大时,直接写出此时点A的坐标;
(3)过点A作垂直于![]() 轴的直线交直线
轴的直线交直线![]() 于点C.以C为顶点的抛物线
于点C.以C为顶点的抛物线![]() 与直线
与直线![]() 的另一个交点为点D.
的另一个交点为点D.
①当AC⊥BD时,求![]() 的值;
的值;
②若以A,B,C,D为顶点构成的图形是凸四边形(各个内角度数都小于180°)时,直接写出满足条件的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
小明同学遇到这样一个问题,如图1,AB=AE,∠ABC=∠EAD,AD=mAC,点P在线段BC上,∠ADE=∠ADP+∠ACB,求![]() 的值.
的值.
小明研究发现,作∠BAM=∠AED,交BC于点M,通过构造全等三角形,将线段BC转化为用含AD的式子表示出来,从而求得![]() 的值(如图2).
的值(如图2).
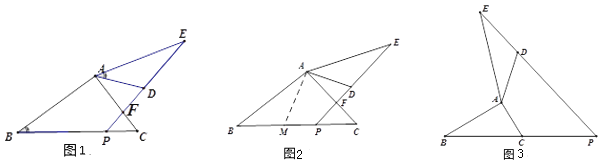
(1)小明构造的全等三角形是:_________≌________;
(2)请你将小明的研究过程补充完整,并求出![]() 的值.
的值.
(3)参考小明思考问题的方法,解决问题:
如图3,若将原题中“AB=AE”改为“AB=kAE”,“点P在线段BC上”改为“点P在线段BC的延长线上”,其它条件不变,若∠ACB=2α,求:![]() 的值(结果请用含α,k,m的式子表示).
的值(结果请用含α,k,m的式子表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,△ABC是等边三角形,点D在BC上,BD=2CD,点F是射线AC上的动点,点M是射线AD上的动点,∠AFM=∠DAB,FM的延长线与射线AB交于点E,设AM=x,△AME与△ABD重叠部分的面积为y,y与x的函数图象如图2所示(其中0<x≤m,m<x<n,x≥n时,函数的解析式不同).
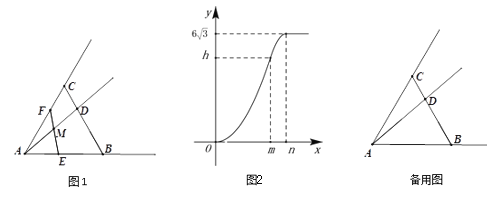
(1)填空:AB=_______;
(2)求出y与x的函数关系式,并求出x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD为菱形,以AD为直径作⊙O交AB于点F,连接DB交⊙O于点H,E是BC上的一点,且BE=BF,连接DE.
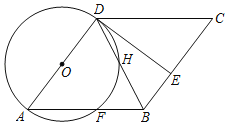
(1)求证:DE是⊙O的切线.
(2)若BF=2,BD=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(1,0)和B(0,3),其顶点为D.设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似
经过点A(1,0)和B(0,3),其顶点为D.设P为该抛物线上一点,且位于抛物线对称轴右侧,作PH⊥对称轴,垂足为H,若△DPH与△AOB相似
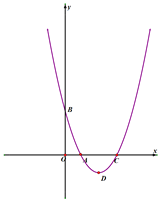
(1)求抛物线的解析式
(2)求点P的坐标
查看答案和解析>>
科目: 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为![]() 米的点
米的点![]() 处.这时,一辆出租车由西向东匀速行驶,测得此车从
处.这时,一辆出租车由西向东匀速行驶,测得此车从![]() 处行驶到
处行驶到![]() 处所用的时间为
处所用的时间为![]() 秒,且
秒,且![]() ,
,![]() .
.

![]() 求
求![]() 、
、![]() 之间的路程;
之间的路程;
![]() 请判断此出租车是否超过了城南大道每小时
请判断此出租车是否超过了城南大道每小时![]() 千米的限制速度?
千米的限制速度?
查看答案和解析>>
科目: 来源: 题型:
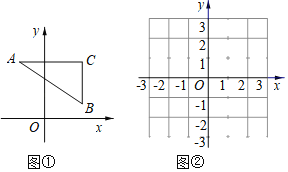
【题目】如图①,在平面直角坐标系中,当线段AB与坐标轴不垂直时,以线段AB为斜边作Rt△ABC,且边BC⊥x轴,则称AC+BC的值为线段AB的直角距离,记作L(AB);当线段AB与坐标轴垂直时,线段AB的直角距离不存在.
(1)在平面直角坐标系中,A(1,4),B(4,2),求L(AB).
(2)在平面直角坐标系中,点A与坐标原点重合,点B(x,y),且L(AB)=2.
①当点B(x,y)在第一象限时,易知AC=x,BC=y.由AC+BC=L(AB),可得y与x之间的函数关系式为 ,其中x的取值范围是 ,在图②中画出这个函数的图象.
②请模仿①的思考过程,分别探究点B在其它象限的情形,仍然在图②中分别画出点B在二、三、四象限时,y与x的函数图象.(不要求写出探究过程)
(3)在平面直角坐标系中,点A(1,1),在抛物线y=a(x﹣h)2+5上存在点B,使得2≤L(AB)≤4.
①当a=﹣![]() 时,直接写出h的取值范围.
时,直接写出h的取值范围.
②当h=0,且△ABC是等腰直角三角形时,直接写出a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com