
科目: 来源: 题型:
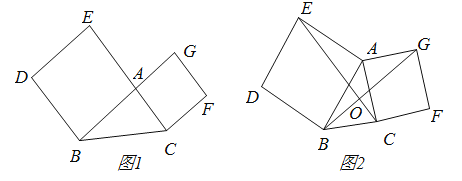
【题目】![]() 如图1,正方形
如图1,正方形![]() 和正方形,
和正方形,![]() 连接
连接![]() ,当
,当![]() 时,
时, ![]() 与
与![]() 的关系是?
的关系是?
![]() 如图2,将正方形
如图2,将正方形![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,![]()
![]() 中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
![]() 已知
已知![]() ,在旋转过程中,若直线
,在旋转过程中,若直线![]() 平分
平分![]() ,请画出相应的图形,并写出其中一种情形时
,请画出相应的图形,并写出其中一种情形时![]() 长的思路.
长的思路.
查看答案和解析>>
科目: 来源: 题型:
【题目】我市某乡镇在“精准扶贫”活动中销售农产品,经分析发现月销售量![]() (万件与月份
(万件与月份![]() (月)的关系为:
(月)的关系为: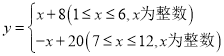
每件产品的利润![]() (元)与月份
(元)与月份![]() (月)的关系如下表:
(月)的关系如下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 10 |
![]() 请你根据表格直接写出每件产品利润z (元) 与月份
请你根据表格直接写出每件产品利润z (元) 与月份![]() (月)的函数关系式;
(月)的函数关系式;
![]() 若月利润
若月利润![]() (万元) =当月销售量
(万元) =当月销售量![]() (万件)
(万件) ![]() 当月每件产品的利润
当月每件产品的利润![]() (元),求月利润
(元),求月利润![]() (万元)与月份
(万元)与月份![]() (月)的关系式;
(月)的关系式;
![]() 当
当![]() 为何值时,月利润
为何值时,月利润![]() 有最大值,最大值为多少?
有最大值,最大值为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】(发现问题)爱好数学的小明在做作业时碰到这样的一道题目:
如图①,点O为坐标原点,⊙O的半径为1,点A(2,0).动点B在⊙O上,连结AB,作等边△ABC(A,B,C为顺时针顺序),求OC的最大值
(解决问题)小明经过多次的尝试与探索,终于得到解题思路:在图①中,连接OB,以OB为边在OB的左侧作等边三角形BOE,连接AE.
(1)请你找出图中与OC相等的线段,并说明理由;
(2)求线段OC的最大值.
(灵活运用)
(3)如图②,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
(迁移拓展)
(4)如图③,BC=4![]() ,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.
,点D是以BC为直径的半圆上不同于B、C的一个动点,以BD为边作等边△ABD,请直接写出AC的最值.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲,乙两人同时各接受了300个零件的加工任务,甲比乙每小时加工的数量多,两人同时开工,其中一人因机器故障停止加工若干小时后又继续按原速加工,直到他们完成任务。如图表示甲比乙多加工的零件数量y(个)与加工时间x(小时)之间的函数关系,观察图象解决下列问题:

(1)其中一人因故障,停止加工_________小时,C点表示的实际意义是________________.甲每小时加工的零件数量为_____________个;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少小时时比甲少加工75个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每小时能加工80个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少小时时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
查看答案和解析>>
科目: 来源: 题型:
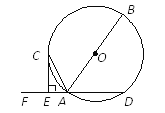
【题目】如图,AB是⊙O的直径,AD是⊙O的弦,点F是DA延长线上的一点,过⊙O上一点C作⊙O的切线交DF于点E,CE⊥DF.
(1)求证:AC平分∠FAB;
(2)若AE=1,CE=2,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,AD=10,请用直尺和圆规按下列步骤作图(不要求写作法,但要保留作图痕迹);

(1)在BC边上作出点E,使得cosBAE![]() .
.
(2)在(1)作出的图形中
①在CD上作出一点F,使得点D、E关于AF对称;
②四边形AEFD的面积=____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com