
科目: 来源: 题型:
【题目】如图所示,一次函数y=x+3与x轴、y轴分别交于点A、B,将直线AB向下平移与反比例函数![]() (x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=
(x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=![]() .
.
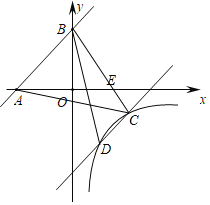
(1)求直线BC和反比例函数解析式;(2)连接BD,求△BCD的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩![]() (单位:分)分成四类:
(单位:分)分成四类:![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() ),
),![]() 类(
类(![]() )绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
)绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
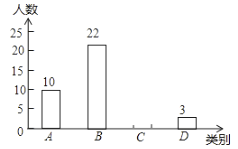
成绩等级 | 人数 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
(1)![]() ______,
______,![]() _______,
_______,![]() _________;
_________;
(2)补全条形统计图;
(3)若该校九年级男生有600名,![]() 类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的交点
轴的交点![]() 与
与![]() 轴交于点
轴交于点![]() .
.
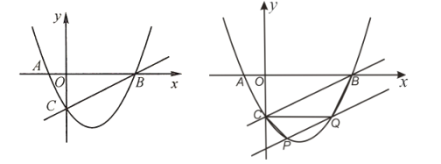
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上的一点,过点
下方抛物线上的一点,过点![]() 作
作![]() 的平行线交抛物线于点
的平行线交抛物线于点![]() (点
(点![]() 在点
在点![]() 右侧),连结
右侧),连结![]() 、
、![]() ,当
,当![]() 的面积为
的面积为![]() 面积的一半时,求
面积的一半时,求![]() 点的坐标;
点的坐标;
(3)现将该抛物线沿射线![]() 的方向进行平移,平移后的抛物线与直线
的方向进行平移,平移后的抛物线与直线![]() 的交点为
的交点为![]() 、
、![]() (点
(点![]() 在点
在点![]() 的下方),与
的下方),与![]() 轴的右侧交点为
轴的右侧交点为![]() ,当
,当![]() 与
与![]() 相似,求出点
相似,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目: 来源: 题型:
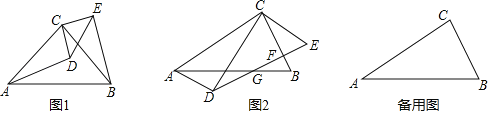
【题目】(1)△ABC和△CDE是两个等腰直角三角形,如图1,其中∠ACB=∠DCE=90°,连结AD、BE,求证:△ACD≌△BCE.
(2)△ABC和△CDE是两个含30°的直角三角形,其中∠ACB=∠DCE=90°,∠CAB=∠CDE=30°,CD<AC,△CDE从边CD与AC重合开始绕点C逆时针旋转一定角度α(0°<α<180°);
①如图2,DE与BC交于点F,与AB交于点G,连结AD,若四边形ADEC为平行四边形,求![]() 的值;
的值;
②若AB=10,DE=8,连结BD、BE,当以点B、D、E为顶点的三角形是直角三角形时,求BE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为更新果树品种,某果园计划新购进![]() 、
、![]() 两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中
两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中![]() 种苗的单价为
种苗的单价为![]() 元/棵,购买
元/棵,购买![]() 种苗所需费用
种苗所需费用![]() (元)与购买数量
(元)与购买数量![]() (棵)之间存在如图所示的函数关系.
(棵)之间存在如图所示的函数关系.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若在购买计划中,![]() 种苗的数量不超过35棵,但不少于
种苗的数量不超过35棵,但不少于![]() 种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目: 来源: 题型:
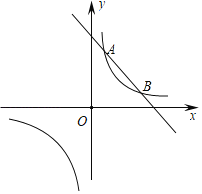
【题目】已知一次函数y=﹣x+m的图象与反比例函数![]() 的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
查看答案和解析>>
科目: 来源: 题型:
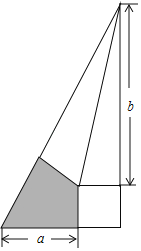
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向点
向点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,两点停止运动,问:
时,两点停止运动,问:
![]() 经过几秒,
经过几秒,![]() 的面积等于
的面积等于![]() ?
?
(2)![]() 的面积会等于
的面积会等于![]() 吗?若会,请求出此时的运动时间;若不会,请说明理由.
吗?若会,请求出此时的运动时间;若不会,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在国家政策的宏观调控下,某市的商品房成交均价由今年3月份的14 000元/m2下降到5月份的12 600元/m2.
(1)问4,5两月平均每月降价的百分率约是多少?(参考数据:![]() ≈0.95)
≈0.95)
(2)如果房价继续跌落,按此降价的百分率,你预测到7月份该市的商品房成交均价是否会跌跛10 000元/m2?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形![]() 的两条边
的两条边![]() 的长是方程
的长是方程![]() 的两根
的两根![]() 沿直线
沿直线![]() 将矩形折叠,点
将矩形折叠,点![]() 落在第一象限的点
落在第一象限的点![]() 处,
处,![]() 交
交![]() 轴于点
轴于点![]() .
.
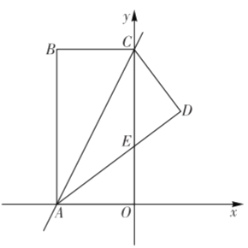
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)将直线![]() 以每秒
以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向下平移,求直线
轴向下平移,求直线![]() 扫过的三角形
扫过的三角形![]() 的面积
的面积![]() 关于运动的时间
关于运动的时间![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,在移动的直线![]() 上是否存在点
上是否存在点![]() ,使以为
,使以为![]() 顶点的四边形是平行四边形?若存在,请直接写出点
顶点的四边形是平行四边形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com