
科目: 来源: 题型:
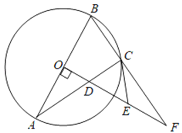
【题目】如图,△ABC内接于⊙O,AB为直径,作OD⊥AB交AC于点D,延长BC,OD交于点F,过点C作⊙O的切线CE,交OF于点E.
(1)求证:EC=ED;
(2)如果OA=4,EF=3,求弦AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃3、4、5三张牌,小明先抽一张,记录后放回,小刚再从3张中随机抽一张,若两张牌上的数字之积是奇数,则小明看电影,否则小刚看电影,乙的方案公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
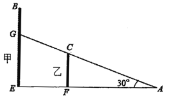
【题目】如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路夹角为30°;
(1)汽车行驶到什么位置时,司机刚好看不到甲建筑物?请在图中标出这个D点;
(2)若CF的高度40米,当刚好看不到甲建筑物时,司机的视线与与公路夹角为45°,请问汽车行驶了多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
⑴求v关于t的函数表达式;
⑵方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
(1)将△ABC绕着O顺时针旋转90°得到△A1B1C1,请画出△A1B1C1,并写出A1的坐标;
(2)以原点O为位似中心,在第一象限画出△A1B1C1的位似图形△A2B2C2,相似比为1:2,并写出A2的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知Rt△ABC中,∠B=90°,∠A=60°,AC=2![]() +4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.
+4,点M、N分别在线段AC、AB上,将△ANM沿直线MN折叠,使点A的对应点D恰好落在线段BC上,当△DCM为直角三角形时,折痕MN的长为__.

查看答案和解析>>
科目: 来源: 题型:
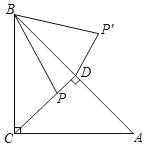
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目: 来源: 题型:
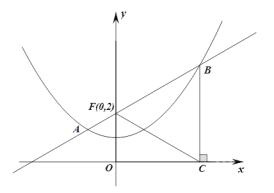
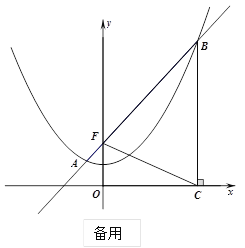
【题目】如图,已知抛物线![]() 过点
过点![]() ,过定点
,过定点![]() 的直线
的直线![]() :
:![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,过点
的右侧,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
(1)求抛物线的解析式;
(2)设点![]() 在x轴上运动,连接
在x轴上运动,连接![]() ,作
,作![]() 的垂直平分线与过点D作x轴的垂线交于点
的垂直平分线与过点D作x轴的垂线交于点![]() ,判断点
,判断点![]() 是否在抛物线
是否在抛物线![]() 上,并证明你的判断;
上,并证明你的判断;
(3)若![]() ,设
,设![]() 的中点为
的中点为![]() ,抛物线上是否存在点
,抛物线上是否存在点![]() ,使得
,使得![]() 周长最小,若存在求出周长的最小值,若不存在说明理由;
周长最小,若存在求出周长的最小值,若不存在说明理由;
(4)若![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() 的面积为
的面积为![]() ,若存在求出点
,若存在求出点![]() 的坐标,若不存在说明理由.
的坐标,若不存在说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】受“新冠”疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对手写板的需求激增.重庆某厂家准备3月份紧急生产A,B两种型号的手写板,若生产20个A型号和30个B型号手写板,共需要投入36000元;若生产30个A型号和20个B型号手写板,共需要投入34000元.
(1)请问生产A,B两种型号手写板,每个各需要投入多少元的成本?
(2)经测算,生产的A型号手写板每个可获利200元,B型号手写板每个可获利400元,该厂家准备用10万元资金全部生产这两种手写板,总获利w元,设生产了A型号手写板a个,求w关于a的函数关系式;
(3)在(2)的条件下,若要求生产A型号手写板的数量不能少于B型号手写板数量的2倍,请你设计出总获利最大的生产方案,并求出最大总获利.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com