【题目】如图，在平面直角坐标系中，的半径为5，点A的坐标为(3，0)，与x轴相交于点B，C，交y轴正半轴于点D．

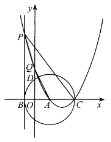
（1）求点B，D的坐标；

（2）过点B作的切线，与过点A，C的抛物线交于点P．抛物线交y轴正半轴于点Q．若P的纵坐标为t，四边形PQAC的面积为y．

①求y与t的函数关系式；

②若△PBO与△DOA相似，求取最小值时m的值．

(1)求y与x之间的函数表达式，并写出x的取值范围；

(2)若该节能产品的日销售利润为W(元)，求W与x之间的函数表达式，并求出日销售利润不超过1040元的天数共有多少天？

(3)若5≤x≤17，直接写出第几天的日销售利润最大，最大日销售利润是多少元？

【题目】我们把有一组对角为直角的四边形叫直方形．设这两个直角的夹边长分别为a，b和c，d，记叫直方形的方周长，如图1．

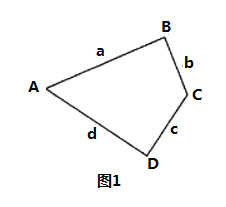
（1）判断与的大小；

（2）如图2，已知点P为双曲线上一动点，过点P作PA⊥x轴交x轴正半轴于点A，以坐标原点O为圆心、OA长为半径作，点B为上不同于点A的点，当以点P，A，O，B为顶点的直方形的方周长取最小值时，求直方形PAOB的面积；

（3）已知直线：与x轴、y轴相交于点A，B，点P为平面上一点，以点P，A，O，B为顶点的直方形的方周长，当反比例函数的图象与直线有两个交点时，求k的取值范围．

【题目】为构建“魅力雨花，和谐雨花，人文雨花”，规划在圭塘河上修建一座观光人行桥（如图1），此工程由桥梁工程与桥上拱形工程组成，桥上拱形工程包含三组完全相同的拱形，观光人行桥的正规图如图2所示，已知桥面上三组拱桥都为相同的抛物线的一部分，拱高（抛物线最高点到桥面的距离）为16米，三条抛物线依次与桥面AB相较于点A，C，D，B．

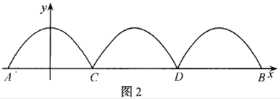
（1）求桥长AB；

（2）已知一组桥拱的造价为a万元，桥面每米的平均造价为b万元．若一组桥拱的造价为整个桥面造价的，这座观光桥的总造价为504万元，求a，b的值．

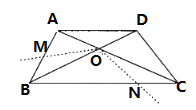
（1）求出sin∠DBC的值；

（2）若AD=2，把∠BOC绕点O顺时针旋转（），交AB于点M，交BC于点N（如图），求证：四边形OMBN的面积为一个定值，并求出这个定值．

（1）分数段在-----范围的人数最多；

（2）全校共有多少人参加比赛？

（3）学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛，并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子．请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果，并求出上衣和能搭配成同一种颜色的概率．

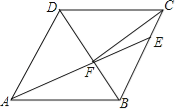
【题目】如图，在菱形ABCD中，AB=6，∠DAB=60°，AE分别交BC、BD于点E、F，CE=2，连接CF，以下结论：①△ABF≌△CBF；②点E到AB的距离是2；③tan∠DCF=；④△ABF的面积为．其中一定成立的是 （把所有正确结论的序号都填在横线上）．

A. ﹣2＜m＜ B. ﹣3＜m＜﹣ C. ﹣3＜m＜﹣2 D. ﹣3＜m＜﹣

【题目】如图，在平面直角坐标系中，抛物线经过B（3，0），C（0，-3）两点，点D为顶点．

（1）求抛物线的解析式及顶点D的坐标；

（2）点E在抛物线的对称轴上，F在BD上，求BE+EF的最小值；

（3）点P是抛物线第四象限的点（不与B、C重合），连接PB，以PB为边作正方形BPMN，当点M或N恰好落在对称轴上时，求出对应的P点的坐标（结果保留根号）．

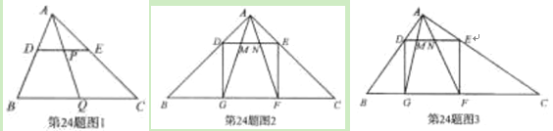
【题目】（本题满分10分）（1）如图1，在△ABC中，点D，E，Q分别在AB，AC，BC上，且DE∥BC，AQ交DE于点P.求证：.

（2）如图，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连接AG，AF分别交DE于M，N两点.

①如图2，若AB=AC=1，直接写出MN的长；

②如图3，求证MN2=DM·EN.