
科目: 来源: 题型:
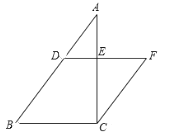
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 6,AC = 8.点D是AB边上一点,过点D作DE // BC,交边AC于E.过点C作CF // AB,交DE的延长线于点F.
(1)如果![]() ,求线段EF的长;
,求线段EF的长;
(2)求∠CFE的正弦值.
查看答案和解析>>
科目: 来源: 题型:
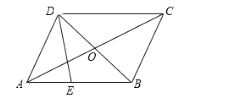
【题目】如图,在平行四边形ABCD中,对角线AC、BD相交于点O.E为边AB上一点,且BE = 2AE.设![]() ,
,![]() .
.
(1)填空:向量![]() ;
;
(2)如果点F是线段OC的中点,那么向量![]() ,并在图中画出向量
,并在图中画出向量![]() 在向量
在向量![]() 和
和![]() 方向上的分向量.
方向上的分向量.
注:本题结果用向量![]() 的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
的式子表示.画图不要求写作法,但要指出所作图中表示结论的向量.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE =________.

查看答案和解析>>
科目: 来源: 题型:
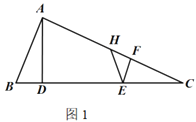
【题目】在图(1)中,在![]() 中,
中,![]() ,垂足为点
,垂足为点![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿射线
的速度沿射线![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时,运动停止.过点
重合时,运动停止.过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,点
,点![]() 在射线
在射线![]() 上的对应点为点
上的对应点为点![]() ,连接
,连接![]() .若
.若![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() ,
,![]() 关于
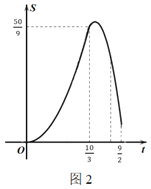
关于![]() 的函数图象如图(2)所示(其中
的函数图象如图(2)所示(其中![]() ,
,![]() ,
,![]() 时,函数解析式不同).
时,函数解析式不同).
(1)求![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列内容,并完成相关问题.
小明定义了一种新的运算,取名为※(加乘)运算.按这种运算进行运算的算式举例如下:
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;![]() .
.
问题:
(1)请归纳※(加乘)运算的运算法则:
两数进行※(加乘)运算时,________.特别地,0和任何数进行※(加乘)运算,或任何数和0进行※(加乘)运算,________.
(2)计算:![]() .(括号的作用与它在有理数运算中的作用一致)
.(括号的作用与它在有理数运算中的作用一致)
(3)我们知道加法有交换律和结合律,这两种运算律在有理数的※(加乘)运算中还适用吗?请任选一个运算律,判断它在※(加乘)运算中是否适用,并举例验证.(举一个例子即可)
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市要进一批鸡蛋进行销售,有![]() 、
、![]() 两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
两家农场可供货.为了比较两家提供的鸡蛋单个大小,超市分别对这两家农场的鸡蛋进行抽样检测,通过分析数据确定鸡蛋的供货商.
(1)下列抽样方式比较合理的是哪一种?请简述原因.
①分别从![]() 、
、![]() 两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
两家提供的一箱鸡蛋中拿出最上面的两层(共40枚)鸡蛋,并分别称出其中每一个鸡蛋的质量.
②分别从![]() 、
、![]() 两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
两家提供的一箱鸡蛋中每一层随机抽4枚(共40枚)鸡蛋,并分别称出其中每个鸡蛋的质量.
(2)在用合理的方法抽出两家提供的鸡蛋各40枚后,分别称出每个鸡蛋的质量(单位:![]() ),结果如表所示(数据包括左端点不包括右端点).
),结果如表所示(数据包括左端点不包括右端点).
45~47 | 47~49 | 49~51 | 51~53 | 53~55 | |
| 2 | 8 | 15 | 10 | 5 |
| 4 | 6 | 12 | 14 | 4 |
①如果从这两家农场提供的鸡蛋中随机拿一个,分别估计两家鸡蛋质量在![]() (单位:
(单位:![]() )范围内的概率(数据包括左端点不包括右端点);
)范围内的概率(数据包括左端点不包括右端点);
②如果你是超市经营者,试通过数据分析确定选择哪家农场提供的鸡蛋.
查看答案和解析>>
科目: 来源: 题型:
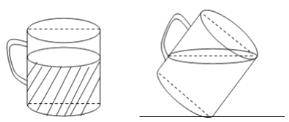
【题目】如图,有一个底面直径与杯高均为![]() 的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈
的杯子里面盛了一些溶液,当它支在桌子上倾斜到液面与杯壁呈![]() 才能将液体倒出,则此时杯子最高处距离桌面________
才能将液体倒出,则此时杯子最高处距离桌面________![]() .(
.(![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙、丙、丁两位同学做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人,则第二次传球后球回到甲手里的概率是________;第三次传球后球回到甲手里的概率是________.
查看答案和解析>>
科目: 来源: 题型:
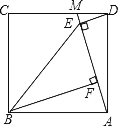
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE,若AF=1,四边形ABED的面积为6,则∠EBF的余弦值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com