
科目: 来源: 题型:
【题目】二次函数y=![]() (x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
(x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
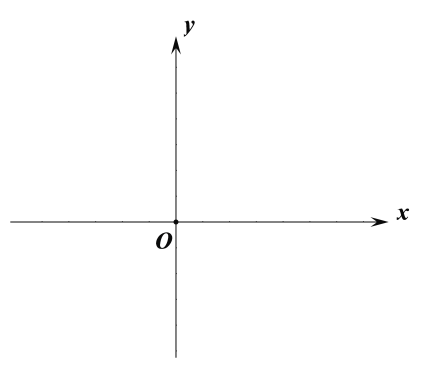
⑴h= ,k= ;
⑵①当点P在顶点时,BC= ;
②BC的值是否随P点横坐标的变化而变化?如果变化,请说明理由,如果不变化,请求出这个值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点B(6,0),与y轴交于点A,与二次函数y=ax2的图象在第一象限内交于点C(3,3).

(1)求此一次函数与二次函数的表达式;
(2)若点D在线段AC上,与y轴平行的直线DE与二次函数图象相交于点E,∠ADO=∠OED,求点D坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据完全平方公式可以作如下推导(a、b都为非负数)
∵ a-2![]() +b=(
+b=(![]() -
-![]() )2≥0 ∴ a-2
)2≥0 ∴ a-2![]() +b≥0
+b≥0
∴ a+b≥2![]() ∴
∴ ![]() ≥
≥![]()
其实,这个不等关系可以推广,![]() ≥
≥![]()
![]()
![]()
… …
![]() (以上an都是非负数)
(以上an都是非负数)
我们把这种关系称为:算术—几何均值不等式
例如:x为非负数时,![]() ,则
,则![]() 有最小值.
有最小值.
再如:x为非负数时,x+x+![]() .
.
我们来研究函数:![]()

(1)这个函数的自变量x的取值范围是 ;
(2)完成表格并在坐标系中画出这个函数的大致图象;
x | … | -3 | -2 | -1 |
|
| 1 | 2 | 3 | … |
y | … |
| 3 |
|
| 5 |
| … |
(3)根据算术—几何均值不等式,该函数在第一象限有最 值,是 ;
(4)某同学在研究这个函数时提出这样一个结论:当x>a时,y随x增大而增大,则a的取值范围是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C为⊙O上一点,BG与⊙O相切于点B,交AC的延长线于点D(点D在线段BG上),AC = 8,tan∠BDC =![]()
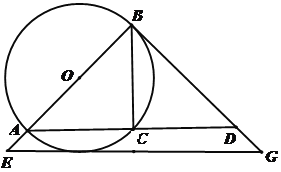
(1)求⊙O的直径;
(2)当DG=![]() 时,过G作
时,过G作![]() ,交BA的延长线于点E,说明EG与⊙O相切.
,交BA的延长线于点E,说明EG与⊙O相切.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某市初中学生课外阅读情况,调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查,并根据调查结果绘制成如下统计图.
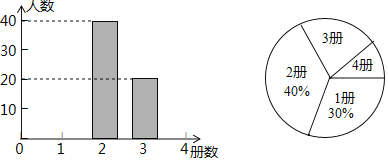
根据统计图提供的信息,解答下列问题:
(1)本次抽样调查的样本容量是 ;
(2)补全条形统计图;
(3)该市共有12000名初中生,估计该市初中学生这学期课外阅读超过2册的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,过
,过![]() 点的直线
点的直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线
,与抛物线![]() 的另一个交点为
的另一个交点为![]() ,己知
,己知![]() ,
,![]() ,
,![]() 点为抛物线
点为抛物线![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合).
重合).
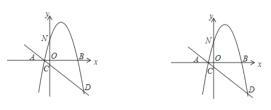
(1)直接写出抛物线和直线![]() 的解析式;
的解析式;
(2)当点![]() 在直线
在直线![]() 上方的抛物线上时,连接
上方的抛物线上时,连接![]() 、
、![]() ,
,
①当![]() 的面积最大时,
的面积最大时,![]() 点的坐标是________;
点的坐标是________;
②当![]() 平分
平分![]() 时,求线段
时,求线段![]() 的长.
的长.
(3)设![]() 为直线
为直线![]() 上的点,探究是否存在点
上的点,探究是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() ,
,![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,直接写出点
为顶点的四边形为平行四边形?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面的材料:
如果函数![]() 满足:对于自变量
满足:对于自变量![]() 的取值范围内的任意
的取值范围内的任意![]() ,
,![]() ,
,
(1)若![]() ,都有
,都有![]() ,则称
,则称![]() 是增函数;
是增函数;
(2)若![]() ,都有
,都有![]() ,则称
,则称![]() 是减函数.
是减函数.
例题:证明函数![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .∴
.∴![]() .即
.即![]() .
.
∴![]() .∴函数
.∴函数![]() (
(![]() )是减函数.
)是减函数.
根据以上材料,解答下面的问题:
己知函数![]() (
(![]() ),
),
(1)计算:![]() _______,
_______,![]() _______;
_______;
(2)猜想:函数![]() (
(![]() )是_______函数(填“增”或“减”);
)是_______函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销![]() 件.已知产销两种产品的有关信息如下表:
件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(件) |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中![]() 为常数,且
为常数,且![]() .
.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与
与![]() 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com