
科目: 来源: 题型:
【题目】已知函数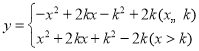 ,(
,(![]() 为常数).
为常数).
(1)当![]() 时,
时,
①求此函数图象与![]() 轴交点坐标.
轴交点坐标.
②当函数![]() 的值随
的值随![]() 的增大而增大时,自变量
的增大而增大时,自变量![]() 的取值范围为________.
的取值范围为________.
(2)若已知函数经过点(1,5),求![]() 的值,并直接写出当
的值,并直接写出当![]() 时函数
时函数![]() 的取值范围.
的取值范围.
(3)要使已知函数![]() 的取值范围内同时含有
的取值范围内同时含有![]() 和
和![]() 这四个值,直接写出
这四个值,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
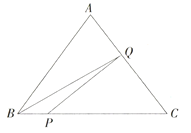
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,同时点Q从点C出发,沿折线
,点P从点B出发,沿BC以每秒2个单位长度的速度向终点C运动,同时点Q从点C出发,沿折线![]() 以每秒5个单位长度的速度运动,到达点A时,点Q停止1秒,然后继续运动.分别连结PQ、BQ.设
以每秒5个单位长度的速度运动,到达点A时,点Q停止1秒,然后继续运动.分别连结PQ、BQ.设![]() 的面积为S,点P的运动时间为
的面积为S,点P的运动时间为![]() 秒.
秒.
(1)求点A与BC之间的距离.
(2)当![]() 时,求
时,求![]() 的值.
的值.
(3)求S与![]() 之间的函数关系式.
之间的函数关系式.
(4)当线段PQ与![]() 的某条边垂直时,直接写出
的某条边垂直时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】教材呈现:下图是华师版九年级上册数学教材第77页的部分内容.
猜想
如图,在![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 与
与![]() 的中点.根据画出的图形,可以猜想:
的中点.根据画出的图形,可以猜想:
![]() ,且
,且![]() .
.
对此,我们可以用演绎推理给出证明.

定理证明:请根据教材内容,结合图①,写出证明过程.
定理应用:
在矩形ABCD中,![]() ,AC为矩形ABCD的对角线,点E在边AB上,且
,AC为矩形ABCD的对角线,点E在边AB上,且![]() .
.
(1)如图②,点F在边CB上,连结EF.若![]() ,则EF与AC的关系为______________.
,则EF与AC的关系为______________.
(2)如图③,将线段AE绕点A旋转一定的角度![]() ,得到线段
,得到线段![]() ,连结
,连结![]() ,点H为
,点H为![]() 的中点,连结BH.设BH的长度为
的中点,连结BH.设BH的长度为![]() .若
.若![]() ,则
,则![]() 的取值范围为___________.
的取值范围为___________.

查看答案和解析>>
科目: 来源: 题型:
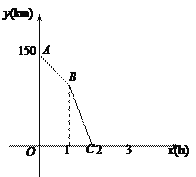
【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
查看答案和解析>>
科目: 来源: 题型:
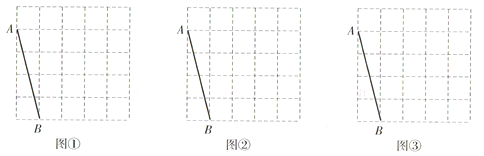
【题目】图①、图②、图③均是5×5的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,不要求写出画法,保留作图痕迹.
(1)在图①中以线段AB为腰画一个等腰直角三角形ABC.所画![]() 的面积为________.
的面积为________.
(2)在图②中以线段AB为斜边画一个等腰直角三角形ABD.
(3)在图③中以线段AB为边画一个![]() ,使
,使![]() ,其面积为
,其面积为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人数(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)这天部分出行学生使用共享单车次数的众数是_________(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,AB是直径,AP是过点A的切线,点C在
中,AB是直径,AP是过点A的切线,点C在![]() 上,点D在AP上,且
上,点D在AP上,且![]() ,延长DC交AB于点E.
,延长DC交AB于点E.
(1)求证:![]() .
.
(2)若![]() 的半径为5,
的半径为5,![]() ,求
,求![]() 的长.(结果保留
的长.(结果保留![]() )
)

查看答案和解析>>
科目: 来源: 题型:
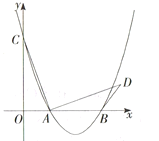
【题目】如图,在平面直角坐标系中,抛物线![]() (
(![]() 是常数,且
是常数,且![]() )与
)与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() .连结
.连结![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连结
,连结![]() .当
.当![]() 最短时,
最短时,![]() 的值为_________ .
的值为_________ .
查看答案和解析>>
科目: 来源: 题型:
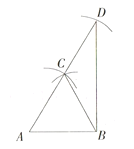
【题目】如图,![]() ,分别以点A、B为圆心,AB长为半径画圆弧,两圆弧交于点C,再以点C为圆心,以AB长为半径画圆弧交AC的延长线于点D,连结BD、BC,则
,分别以点A、B为圆心,AB长为半径画圆弧,两圆弧交于点C,再以点C为圆心,以AB长为半径画圆弧交AC的延长线于点D,连结BD、BC,则![]() 的面积是___________
的面积是___________
查看答案和解析>>
科目: 来源: 题型:
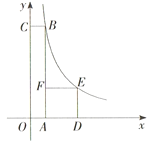
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,四边形
是矩形,四边形![]() 是正方形,点
是正方形,点![]() 、
、![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在函数
在函数![]() 的图象上,若正方形
的图象上,若正方形![]() 的面积为4,且
的面积为4,且![]() ,则
,则![]() 的值为( )
的值为( )
A.24B.12C.6D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com