
科目: 来源: 题型:
【题目】如图,已知菱形ABCD的顶点A(0,﹣1),∠DAC=60°.若点P从点A出发,沿A→B→C→D→A…的方向,在菱形的边上以每秒0.5个单位长度的速度移动,则第2020秒时,点P的坐标为( )
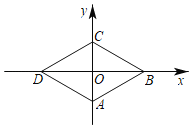
A.(2,0)B.(![]() ,0)C.(﹣
,0)C.(﹣![]() ,0)D.(0,1 )
,0)D.(0,1 )
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是菱形,BC∥x轴.AD与y轴交于点E,反比例函数y=![]() (x>0)的图象经过顶点C、D,已知点C的横坐标为5,BE=3DE,则k的值为( )
(x>0)的图象经过顶点C、D,已知点C的横坐标为5,BE=3DE,则k的值为( )
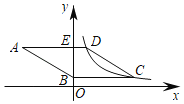
A.![]() B.
B.![]() C.3D.5
C.3D.5
查看答案和解析>>
科目: 来源: 题型:
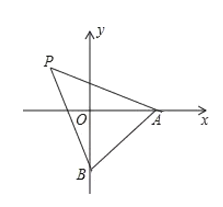
【题目】如图1,已知点![]() ,
,![]() 、
、![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)若![]() ,则
,则![]() _______,此时
_______,此时![]() ________.
________.
(2)求![]() 的面积.
的面积.
(3)在线段![]() 上取一点
上取一点![]() 使
使![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得四边形
,使得四边形![]() 是平行四边形,如果存在,请直接写出点
是平行四边形,如果存在,请直接写出点![]() 的横坐标,如果不存在,请说明理由.
的横坐标,如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,抛物线与
的左侧,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
(1)求抛物线的函数表达式;
(2)设![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为线段
为线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() 及抛物线于点
及抛物线于点![]() 、点
、点![]() ,当
,当![]() 是锐角三角形时,求
是锐角三角形时,求![]() 的取值范围.
的取值范围.
(3)在(2)的前提下,设![]() ,求
,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅行团32人在景区A游玩,他们由成人、少年和儿童组成.已知儿童10人,成人比少年多12人.
(1)求该旅行团中成人与少年分别是多少人?
(2)因时间充裕,该团准备让成人和少年(至少各1名)带领10名儿童去另一景区B游玩.景区B的门票价格为100元/张,成人全票,少年8折,儿童6折,一名成人可以免费携带一名儿童.
①若由成人8人和少年5人带队,则所需门票的总费用是多少元?
②若剩余经费只有1200元可用于购票,在不超额的前提下,最多可以安排成人和少年共多少人带队?求所有满足条件的方案,并指出哪种方案购票费用最少.
查看答案和解析>>
科目: 来源: 题型:
【题目】2020春开学为防控冠状病毒,学生进校园必须戴口罩,测体温,某校开通了三条人工测体温的通道,每周一分别由王老师、张老师、李老师三位老师给进校园的学生测体温(每个通道一位老师),周一有两学生进校园,在3个通道中,可随机选择其中的一个通过.
(1)其中一个学生进校园时,由王老师测体温的概率是_________;
(2)求两学生进校园时,都是王老师测体温的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】目前,我国的空气质量得到了大幅度的提高.现随机调查了某城市1个月的空气质量情况,并将监测的结果绘制成如下的两幅不完整的统计图.
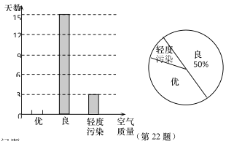
请根据图中提供的信息,解答下面的问题:
(1)本次调查中,一共调查的天数为_______天;扇形图中,表示“轻度污染”的扇形的圆心角为______度;
(2)将条形图补充完整;
(3)估计该城市一年(以365天计算)中,空气质量未达到优的天数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,曲线![]() 是抛物线
是抛物线![]() 的一部分(其中
的一部分(其中![]() 是抛物线与
是抛物线与![]() 轴的交点,
轴的交点,![]() 是顶点),曲线
是顶点),曲线![]() 是双曲线
是双曲线![]() 的一部分.曲线
的一部分.曲线![]() 与
与![]() 组成图形
组成图形![]() .由点
.由点![]() 开始不断重复图形
开始不断重复图形![]() 形成一组“波浪线”.若点
形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则
在该“波浪线”上,则![]() 的最大值为( )
的最大值为( )
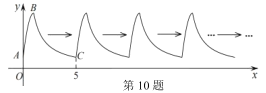
A.5B.6C.2020D.2021
查看答案和解析>>
科目: 来源: 题型:
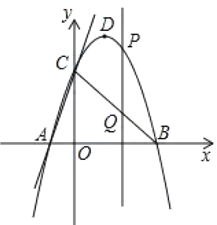
【题目】如图,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 在
在![]() 轴上,
轴上,![]() 为抛物线
为抛物线![]() 的顶点.
的顶点.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)若![]() 是第一象限内抛物线上的一个运动的点,点
是第一象限内抛物线上的一个运动的点,点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,求当
,求当![]() 为何值时,线段
为何值时,线段![]() 的长最大?最大值是多少?并直接写出此时点
的长最大?最大值是多少?并直接写出此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,当![]() 的长取得最大值时,在坐标平面内是否存在点
的长取得最大值时,在坐标平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点
为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
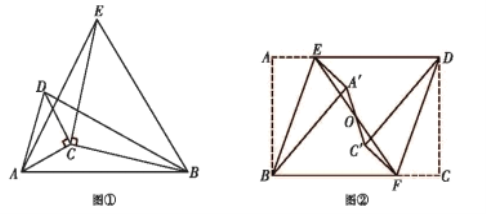
【题目】“综合与实践”是以问题为中心,以活动为平台,以解决某一实际的数学问题为目标,综合应用知识和方法解决问题,它是对数学知识的延伸和发展,是对理解、运用数学基础知识和基本技能的升华过程.请同学们运用你所学的数学知识来研究和解决以下问题吧.
(1)探究:已知![]() 是平面上一个运动的点,若
是平面上一个运动的点,若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;若
的长最小,最小值为 ;若![]() ,
,![]() ,则当点
,则当点![]() 位于 时,线段
位于 时,线段![]() 的长最小,最小值为 ;
的长最小,最小值为 ;
(2)应用:已知![]() 是一运动的点,
是一运动的点,![]() ,
,![]() ,如图①所示,分别以
,如图①所示,分别以![]() 为边作等腰直角三角形
为边作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,且
,且![]() ,连接
,连接![]() 和
和![]() .
.
①在图中找出与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②何时线段![]() 可以取得最小值?请直接写出线段
可以取得最小值?请直接写出线段![]() 的最小值;
的最小值;
(3)拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为矩形
为矩形![]() 对角线的交点,
对角线的交点,![]() 为
为![]() 边上任意一点,连接
边上任意一点,连接![]() 并延长与
并延长与![]() 边交于点
边交于点![]() ,现将图中
,现将图中![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 分别落在矩形
分别落在矩形![]() 内的点
内的点![]() ,
,![]() 处,连接
处,连接![]() ,则
,则![]() 的长有最小值吗?若有,请直接写出
的长有最小值吗?若有,请直接写出![]() 的长的最小值;若没有,请说明理由.
的长的最小值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com