
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
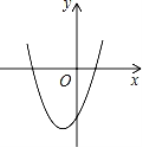
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线![]() 的对称轴是直线
的对称轴是直线![]() 且与
且与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 是第一象限内抛物线上一点,过点
是第一象限内抛物线上一点,过点![]() 作直线
作直线![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 当
当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
![]() 在
在![]() 的条件下,若点
的条件下,若点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,当以点
在抛物线的对称轴上,当以点![]() 为顶点的四边形是平行四边形时,求出所有符合条件的点
为顶点的四边形是平行四边形时,求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
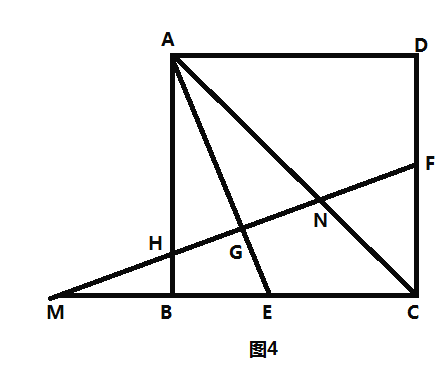
【题目】如图1,在矩形![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,点
上,点![]() 分别在边
分别在边![]() 上,且
上,且![]() .
.
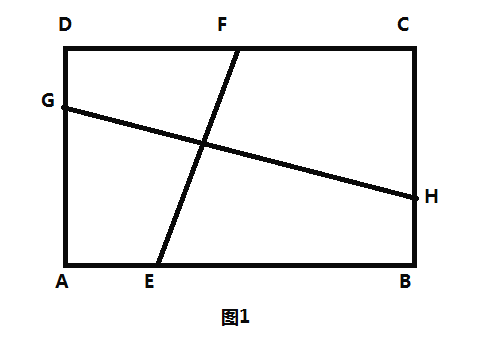
![]() 如图2,过点
如图2,过点![]() 作
作![]() 于点
于点![]() 过点
过点![]() 作
作![]() 于点
于点![]() 可知四边形
可知四边形![]() 四边形
四边形![]() 四边形
四边形![]() 四边形
四边形![]() 都是矩形,即
都是矩形,即![]()
![]() ,通过证明
,通过证明![]() 可求得
可求得![]() 的值为_ .
的值为_ .
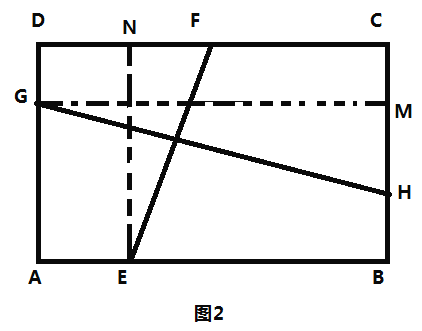
![]() 如图3,在正方形
如图3,在正方形![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() 于点
于点![]() ,则
,则![]() 的值为 .
的值为 .
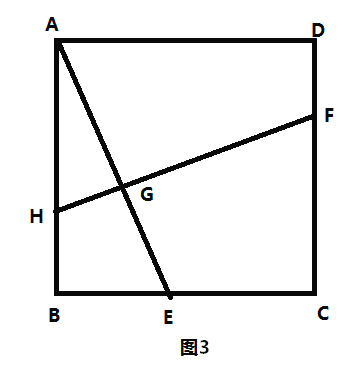
![]() 如图4,在
如图4,在![]() 的条件下,延长
的条件下,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() 连接
连接![]() 交
交![]() 于点
于点![]() .若
.若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】运城菖蒲酒产于山西垣曲.莒蒲洒远在汉代就已名噪酒坛,为历代帝王将相所喜爱,并被列为历代御膳香醪.菖蒲酒在市场的销售量会根据价格的变化而变化.菖蒲酒每瓶的成本价是![]() 元,某超市将售价定为
元,某超市将售价定为![]() 元时,每天可以销售
元时,每天可以销售![]() 瓶,若售价每降低
瓶,若售价每降低![]() 元,每天即可多销售
元,每天即可多销售![]() 瓶(售价不能高于
瓶(售价不能高于![]() 元),若设每瓶降价
元),若设每瓶降价![]() 元
元
![]() 用含
用含![]() 的代数式表示菖蒲酒每天的销售量.
的代数式表示菖蒲酒每天的销售量.
![]() 每瓶菖蒲酒的售价定为多少元时每天获取的利润最大?最大利润是多少?
每瓶菖蒲酒的售价定为多少元时每天获取的利润最大?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市将举办“时代新人说”第三季,幸福园小区居委会为了解居民获取“时代新人说”活动相关信息的方式进行了随机抽样调查,调查设置了A(网络),B(电视),C(报纸),D(其他)四种方式,被调查的居民只能从中选取一种方式,并根据收集到的数据绘制了如下的两幅均不完整的统计图:
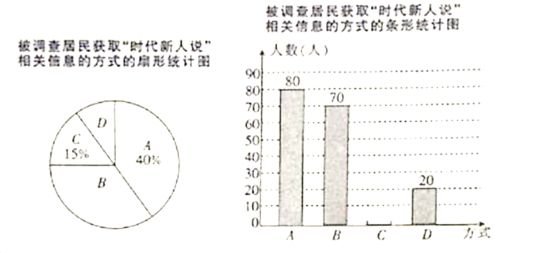
根据图中信息,解答下列问题.
![]() 补全上面的条形统计图.
补全上面的条形统计图.
![]() 在扇形统计图中,选择
在扇形统计图中,选择![]() 种方式的人数所占的百分比是 ,选择
种方式的人数所占的百分比是 ,选择![]() 种方式的人数所在扇形圆心角的度数是 .
种方式的人数所在扇形圆心角的度数是 .
![]() 该小区有
该小区有![]() 男
男![]() 女报名了社区的“时代新人说”活动,由于人数限制,居委会只能从中随机抽取
女报名了社区的“时代新人说”活动,由于人数限制,居委会只能从中随机抽取![]() 名参加活动,请你用画树状图或列表的方法求出恰好抽到
名参加活动,请你用画树状图或列表的方法求出恰好抽到![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC 中,∠C=90°,以BC为直径的半圆交AB于点D,O是该半圆所在圆的圆心,E为线段AC上一点,且ED=EA.
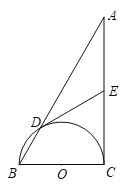
(1)求证:ED是⊙O的切线;
(2)若![]() ,∠A=30°,求⊙O的半径.
,∠A=30°,求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解某校九年级学生的课外数学学习时长情况,该校将选取部分学生进行调查,以下样本中,最具代表性的是( )
A.该年级篮球社团的学生
B.该年级数学成绩前![]() 名的女生
名的女生
C.该年级跑步较快的学生
D.从每个班级中,抽取学号为![]() 的整数倍的学生
的整数倍的学生
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,![]() )三点.
)三点.

(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=![]() (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式k2x+b﹣![]() >0的解集.
>0的解集.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com