【题目】二次函数的部分图象如图③所示，图象过点(－1，0)，对称轴为直线＝2，则下列结论中正确的个数有( )

①4＋b＝0；②；③若点A(－3， )，点B(－， )，点C(5， )在该函数图象上，则＜＜；④若方程的两根为和，且＜，则＜－1＜5＜.

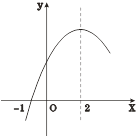
A. 1个 B. 2个 C. 3个 D. 4个

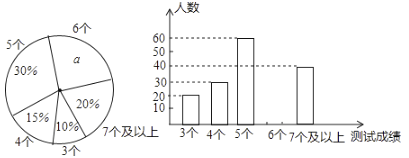
请你根据相关信息，解答下列问题：

（1）写出扇形图中___________，并补全条形图；

（2）求本次调查获取的样本数据的平均数、众数和中位数；

（3）该区体育中考选报引体向上的男生共有1800人，如果体育中考引体向上达6个以上（含6个）得满分，请你估计该区体育中考中选报引体向上的男生能获得满分的有多少人？

【题目】某工厂计划招聘两个工种的工人共120人，两个工种的工人月工资分别为3200元和4000元．

（1）若某工厂每月支付工人的工资为440000元，那么两个工种的工人各招聘多少人？设招聘工种的工人人，填写下表，并列方程求解；

（2）设工厂每月支付工人的工资为元，试写出与之间的函数表达式，若要求工种的人数不少于工种人数的2倍，那么招聘工种的工人多少人时，可使工厂每月支付的工人工资最少？

【题目】将一个直角三角形纸片，放置在平面直角坐标系中，点，点，点

(I)过边上的动点 (点不与点，重合)作交于点，沿着折叠该纸片，点落在射线上的点处．

①如图，当为中点时，求点的坐标；

②连接，当为直角三角形时，求点坐标：

(Ⅱ)是边上的动点(点不与点重合)，将沿所在的直线折叠，得到，连接，当取得最小值时，求点坐标(直接写出结果即可)．

【题目】二次函数（是常数，）的图象与轴交于点和点（点在点的右侧），与轴交于点，连接．

（1）用含的代数式表示点和点的坐标；

（2）垂直于轴的直线在点与点之间平行移动，且与抛物线和直线分别交于点，设点的横坐标为，线段的长为．

①当时，求的值；

②若，则当为何值时，取得最大值，并求出这个最大值．

【题目】如图所示，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6，那么AC=_____．

【题目】如图，将放在每个小正方形的边长为1的网格中，点，点，点均落在格点上．

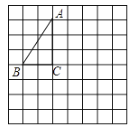
（1）_________．

（2）请在如图所示的网格中，用无刻度的直尺，画出一个以为底边的等腰，使该三角形的面积等于的面积，并简要说明点的位置是如何找到的（不要求证明）__________．

（1）求k的值；

（2）设抛物线与直线y＝﹣（x﹣3）（m≠0）两交点的横坐标为x1，x2，n＝x1+x2﹣2，若A（1，a），B（b，）两点在动点M（m，n）所形成的曲线上，求直线AB的解析式；

（3）将（2）中的直线AB绕点（3，0）顺时针旋转45°，与抛物线x轴上方的部分相交于点C，请直接写出点C的坐标．

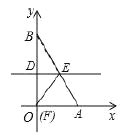
【题目】将一个直角三角形纸片，放置在平面直角坐标系中，点，点，点

(I)过边上的动点 (点不与点，重合)作交于点，沿着折叠该纸片，点落在射线上的点处．

①如图，当为中点时，求点的坐标；

②连接，当为直角三角形时，求点坐标：

(Ⅱ)是边上的动点(点不与点重合)，将沿所在的直线折叠，得到，连接，当取得最小值时，求点坐标(直接写出结果即可)．

【题目】某公司有甲种原料，乙种原料，计划用这两种原料生产、两种产品共40件．生产每件种产品需甲种原料，乙种原料，可获利润900元；生产每件种产品需甲种原料，乙种原料，可获利润1100元．设安排生产种产品件(为非负整数)． ．

(I)根据题意，填写下表：

(Ⅱ) 安排生产、两种产品的件数有几种方案？试说明理由：

(Ⅲ) 设生产这批40件产品共可获利润元，将表示为的函数，并求出最大利润．