
科目: 来源: 题型:
【题目】![]() 地和
地和![]() 地之间有一条笔直的公路,一天,甲车从
地之间有一条笔直的公路,一天,甲车从![]() 地去
地去![]() 地,乙车从
地,乙车从![]() 地去
地去![]() 地,乙先出发,若甲、乙之间的距离为
地,乙先出发,若甲、乙之间的距离为![]() 千米,行驶时间为
千米,行驶时间为![]() 小时,
小时,![]() 与
与![]() 之间的函数关系如图所示,则下列说法错误的是 ( )
之间的函数关系如图所示,则下列说法错误的是 ( )

A.![]() 两地间距离为100千米B.甲车的速度是80千米/时
两地间距离为100千米B.甲车的速度是80千米/时
C.甲到![]() 地比乙车到
地比乙车到![]() 地早
地早![]() 小时D.甲出发0.5小时后与乙车相遇
小时D.甲出发0.5小时后与乙车相遇
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径在其左侧作半圆
为半径在其左侧作半圆![]() ,分别交
,分别交![]() )于点
)于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
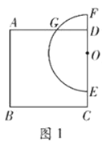
(1)![]() ;
;
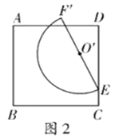
(2)如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为
的对应点为![]() ;设
;设![]() 为半圆
为半圆![]() 上一点.
上一点.
①当点![]() 落在
落在![]() 边上时,求点
边上时,求点![]() 与线段
与线段![]() 之间的最短距离;
之间的最短距离;
②当半圆![]() 交
交![]() 于
于![]() 两点时,若
两点时,若![]() 的长为
的长为![]() ,求此时半圆
,求此时半圆![]() 与正方形
与正方形![]() 重叠部分的面积;
重叠部分的面积;
③当半圆![]() 与正方形
与正方形![]() 的边相切时,设切点为
的边相切时,设切点为![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,我们定义:横坐标与纵坐标均为整数的点为整点如图,已知双曲线![]() 经过点
经过点![]() ,记双曲线与两坐标轴之间的部分为
,记双曲线与两坐标轴之间的部分为![]() (不含双曲线与坐标轴).
(不含双曲线与坐标轴).
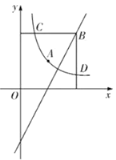
(1)求![]() 的值;
的值;
(2)求![]() 内整点的个数;
内整点的个数;
(3)设点![]() 在直线
在直线![]() 上,过点
上,过点![]() 分别作平行于
分别作平行于![]() 轴
轴![]() 轴的直线,交双曲线
轴的直线,交双曲线![]()
![]() 于点
于点![]() ,记线段
,记线段![]() 、双曲线所围成的区域为
、双曲线所围成的区域为![]() ,若
,若![]() 内部(不包括边界)不超过
内部(不包括边界)不超过![]() 个整点,求
个整点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形![]() 中,点
中,点![]() 是边
是边![]() 上一点(不与点
上一点(不与点![]() 重合),点
重合),点![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
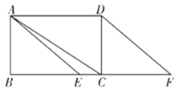
(1)求证:![]()
(2)连接![]() ,其中
,其中![]()
①当四边形![]() 是菱形时,求线段
是菱形时,求线段![]() 与线段
与线段![]() 之间的距离;
之间的距离;
②若点![]() 是
是![]() 的内心,连接
的内心,连接![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
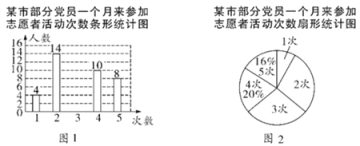
(1) “![]() 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;
(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于![]() 次的概率;
次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为![]() ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为![]() ,当
,当![]() 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在证明定理“三角形的中位线平行于第三边,且等于第三边的一半”时,小明给出如下部分证明过程.
已知:在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点.
的中点.
求证: .
证明:如图,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
,
···
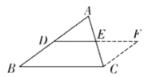
(1)补全求证:
(2)请根据添加的辅助线,写出完整的证明过程;
(3)若![]() 求边
求边![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于题目:在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 且平行
且平行![]() 轴的直线与过点
轴的直线与过点![]() 且平行
且平行![]() 轴的直线相交于点
轴的直线相交于点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有唯一公共点,求
有唯一公共点,求![]() 的取值范围.甲的计算结果是
的取值范围.甲的计算结果是![]() ;乙的计算结果是
;乙的计算结果是![]() ,则( )
,则( )
A.甲的结果正确B.乙的结果正确
C.甲与乙的结果合在一起正确D.甲与乙的结果合在一起也不正确
查看答案和解析>>
科目: 来源: 题型:
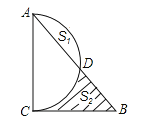
【题目】以△ABC的边AC为直径的半圆交AB边于D点,∠A、∠B、∠C所对边长为a、b、c,且二次函数y=![]() (a+c)x2-bx+
(a+c)x2-bx+![]() (c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(c-a)顶点在x轴上,a是方程z2+z-20=0的根.
(1)证明:∠ACB=90°;
(2)若设b=2x,弓形面积S弓形AED=S1,阴影面积为S2,求(S2-S1)与x的函数关系式;
(3)在(2)的条件下,当BD为何值时,(S2-S1)最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com