
科目: 来源: 题型:
【题目】若一条直线把一个平面图形分成面积相等的两部分,那么这条直线叫做该平面图形的“和谐线”,其“和谐线”被该平面图形截得的线段叫做该平面图形的“和谐线段”(例如圆的直径就是圆的“和谐线段”)
问题探究:
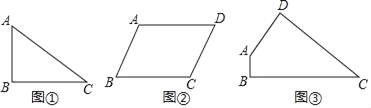
(1)如图①,已知△ABC中,AB=6,BC=8,∠B=90°,请写出△ABC的两条“和谐线段”的长.
(2)如图②,平行四边形ABCD中,AB=6,BC=8,∠B=60°,请直接写出该平行四边形ABCD的“和谐线段”长的最大值和最小值;
问题解决
(3)如图③,四边形ABCD是某市规划中的商业区示意图,其中AB=2,CD=10,∠A=135°,∠B=90°,tanC=![]() ,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
,现计划在商业区内修一条笔直的单行道MN(小道的宽度不计),入口M在BC上,出口N在CD上,使得MN为四边形ABCD“和谐线段”,在道路一侧△MNC区域规划为公园,为了美观要求△MNC是以CM为腰的等腰三角形,请通过计算说明设计师的想法能否实现?若可以,请确定点M的位置(即求CM的长).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:抛物线l,y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,﹣3).
(1)求抛物线l的顶点P的坐标为的A的坐标;
(2)将抛物线l先向上平移3个单位长度,再向左平移2个单位长度,得到抛物线l1,请直接写出平移后的抛物线l1的表达式;
(3)将抛物线l向右平移m个单位长度,得到抛物线l2,其中点A的对应点为点M,若点M、A、P是恰好一个矩形的三个顶点,请求出m的值
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
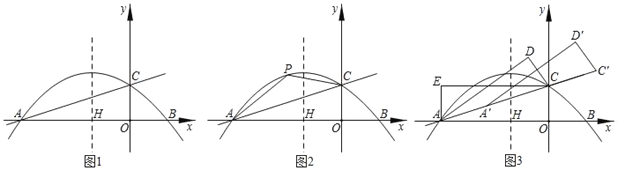
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
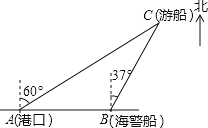
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目: 来源: 题型:
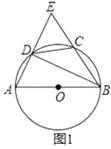
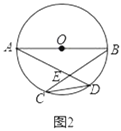
【题目】已知AB是⊙O的直径,AB=2,点C,点D在⊙O上,CD=1,直线AD,BC交于点E.
(Ⅰ)如图1,若点E在⊙O外,求∠AEB的度数;
(Ⅱ)如图2,若点E在⊙O内,求∠AEB的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】植树节期间,某校360名学生参加植树活动,要求每人植树3~6棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:3棵;B:4棵;C:5棵;D:6棵.根据各类型对应的人数绘制了扇形统计图(如图1)和尚未完成的条形统计图(如图2).请解答下列问题:


(1)将条形统计图补充完整;
(2)这20名学生每人植树量的众数为________棵,中位数为________棵;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的:
第一步:求平均数的公式是![]() ;
;
第二步:在该问题中,n=4,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
第三步:![]() .
.
①小宇的分析是不正确的,他错在第几步?
请你帮他计算出正确的平均数,并估计这360名学生共植树多少棵.
查看答案和解析>>
科目: 来源: 题型:
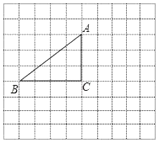
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上
(Ⅰ)线段AB的长度=________;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,在∠ABC的平分线上找一点P,在BC上找一点Q,使CP+PQ的值最小,并简要说明点P,Q的位置是如何找到的_____________(不要求证明).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)经过点(﹣1,0),且满足4a+2b+c>0,有下列结论:①a+b>0;②﹣a+b+c>0;③b2﹣2ac>5a2.其中,正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com