
科目: 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且c>b>a,若Rt△ABC是奇异三角形,求a:b:c;
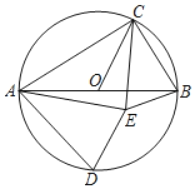
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形:
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目: 来源: 题型:
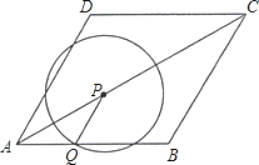
【题目】如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以![]() cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为t(s).
cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB作匀速运动.当P运动到C点时,P、Q都停止运动,设点P运动的时间为t(s).
(1)对角线AC的长是 cm;
(2)当P异于A、C时,请说明PQ∥BC;
(3)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,t为怎样的值时,⊙P与边BC分别有1个公共点和2个公共点?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
(1)若E是CD的中点时,证明:FG是⊙O的切线
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长;若不能,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,C为
为直径,C为![]() 上一点.
上一点.
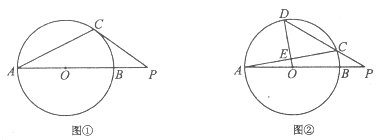
(Ⅰ)如图①,过点C作![]() 的切线,与
的切线,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小;
的大小;
(Ⅱ)如图②,D为弧![]() 的中点,连接
的中点,连接![]() 交
交![]() 于点E,连接
于点E,连接![]() 并延长,与
并延长,与![]() 的延长线相交于点P,若
的延长线相交于点P,若![]() ,求
,求![]() 的大小.
的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
查看答案和解析>>
科目: 来源: 题型:
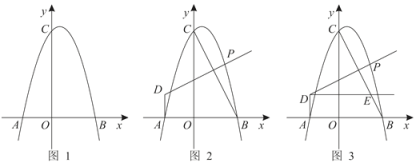
【题目】已知:如图,抛物线![]() 交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
(1)写出a,b,c的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为h.
①求h与t的函数关系式和h的最大值(请求出自变量t的取值范围);
②过第二象限点D作DE∥AB交BC于点E,若DP=CE,时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
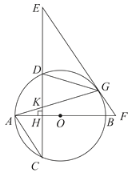
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目: 来源: 题型:
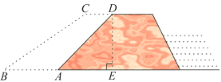
【题目】为做好汉江防汛工作,防汛指挥部决定对一段长为2500m重点堤段利用沙石和土进行加固加宽.专家提供的方案是:使背水坡的坡度由原来的1:1变为1:1.5,如图,若CD∥BA,CD=4米,铅直高DE=8米.
(1)求加固加宽这一重点堤段需沙石和土方数是多少?
(2)某运输队承包这项沙石和土的运送工程,根据施工方计划在一定时间内完成,按计划工作5天后,增加了设备,工效提高到原来的1.5倍,结果提前了5天完成任务,问按原计划每天需运送沙石和土多少m3?
查看答案和解析>>
科目: 来源: 题型:
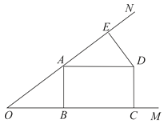
【题目】如图,点A在∠MON的边ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求证:四边形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)请用列表法或树状图写出所有的等可能性结果,写出所有个位数字是6的“两位递增数”;
(2)求抽取的“两位递增数”的个位数字与十位数字之积能被5整除的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com