
科目: 来源: 题型:
【题目】已知:二次函数![]() ,当
,当![]() 时,函数有最大值
时,函数有最大值![]() .
.
(1)求此二次函数图象与坐标轴的交点;
(2)将函数![]() 图象
图象![]() 轴下方部分沿
轴下方部分沿![]() 轴向上翻折,得到的新图象,若点
轴向上翻折,得到的新图象,若点![]() 是翻折得到的抛物线弧部分上任意一点,若关于
是翻折得到的抛物线弧部分上任意一点,若关于![]() 的一元二次方程
的一元二次方程![]() 恒有实数根时,求实数
恒有实数根时,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
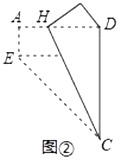
【题目】对给定的一张矩形纸片![]() 进行如下操作:先沿
进行如下操作:先沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上(如图①),再沿
边上(如图①),再沿![]() 折叠,这时发现点
折叠,这时发现点![]() 恰好与点
恰好与点![]() 重合(如图②)
重合(如图②)
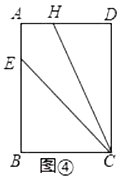
(1)根据以上操作和发现,则![]() ____;
____;
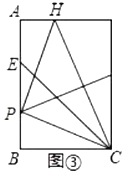
(2)将该矩形纸片展开,如图③,折叠该矩形纸片,使点![]() 与点
与点![]() 重合,折痕与
重合,折痕与![]() 相交于点
相交于点![]() ,再将该矩形纸片展开.
,再将该矩形纸片展开.
求证:![]() ;
;

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场试销一种成本为![]() 元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于
元/件的T 恤,规定试销期间单价不低于成本单价,又获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元/件)符合一次函数
(元/件)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
(1)写出销售单价![]() 的取值范围;
的取值范围;
(2)求出一次函数![]() 的解析式;
的解析式;
(3)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
之间的关系式,销售单价定为多少时,商场可获得最大利润,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
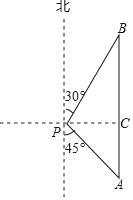
【题目】随着航母编队的成立,我国海军日益强大,2018年4月12日,中央军委在南海海域降重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到1海里).
≈1.732,结果精确到1海里).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
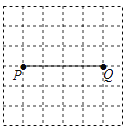
(1)在图1中画出一个面积最小的¨PAQB;
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.

(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目: 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1<m<n<1,则m+n<![]() ;④3|a|+|c|<2|b|.其中正确的结论个数是( )
;④3|a|+|c|<2|b|.其中正确的结论个数是( )
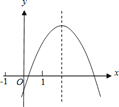
A. ①③④ B. ①③ C. ①④ D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,抛物线y=﹣![]() x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
x2+x+4与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)求直线BD的解析式;
(2)如图②,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() GE的值最小,求出点G的坐标及PG﹣
GE的值最小,求出点G的坐标及PG﹣![]() GE的最小值;
GE的最小值;
(3)将抛物线沿直线AC平移,点A,C平移后的对应点为A′,C'.在平面内有一动点H,当以点B,A',C',H为顶点的四边形为平行四边形时,在直线AC上方找一个满足条件的点H,与直线AC下方所有满足条件的点H为顶点的多边形为轴对称图形时,求出点A′的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如果一个正整数m能写成m=a2﹣b2(a、b均为正整数,且a≠b),我们称这个数为“平方差数”,则a、b为m的一个平方差分解,规定:F(m)=![]() .
.
例如:8=8×1=4×2,由8=a2﹣b2=(a+b)(a﹣b),可得![]() 或
或![]() .因为a、b为正整数,解得
.因为a、b为正整数,解得![]() ,所以F(8)=
,所以F(8)=![]() .又例如:48=132﹣112=82﹣42=72﹣12,所以F(48)=
.又例如:48=132﹣112=82﹣42=72﹣12,所以F(48)=![]() 或
或![]() 或
或![]() .
.
(1)判断:6 平方差数(填“是“或“不是“),并求F(45)的值;
(2)若s是一个三位数,t是一个两位数,s=100x+5,t=10y+x(1≤x≤4,1≤y≤9,x、y是整数),且满足s+t是11的倍数,求F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com