
科目: 来源: 题型:
【题目】2020年年初以来,全国多地猪肉价格连续上涨,引起了民众与政府的高度关注,政府向市场投入储备猪肉进行了价格平抑.据统计:某超市2020年1月10日猪肉价格比去年同一天上涨了40%,这天该超市每千克猪肉价格为56元.

(1)求2019年1月10日,该超市猪肉的价格为每千克多少元?
(2)现在某超市以每千克46元的价格购进猪肉,按2020年1月10日价格出售,平均一天能销售100千克.经调查表明:猪肉的售价每千克下降1元,平均每日销售量就增加20千克,超市为了实现销售猪肉平均每天有1120元的销售利润,在尽可能让利于顾客的前提下,每千克猪肉应该定价为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】2019年11月22日,教育部发布关于《中小学教师实施教育惩戒规则(征求意见稿)》公开征求意见的通知,征求意见稿指出;教育惩戒是教师履行救育教学职责的必要手段和法定职权.教育惩戒分为![]() :一般惩戒,
:一般惩戒,![]() :较重惩戒,
:较重惩戒,![]() :严重惩戒,
:严重惩戒,![]() :强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.
:强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.

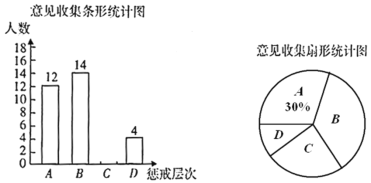
请你根据统计图提供的信息,解答下列问题:
(1)被调查的总人数是______人;
(2)扇形统计图中![]() 部分对应的圆心角的度数为______;
部分对应的圆心角的度数为______;
(3)补全条形统计图;
(4)某班主任对学生进行了纪律教育,要求小明和小军分别从题中所述的四个层次中随机选择一个层次说明惩戒内容.请用列表法或画树状图法求两人选择不同教育惩戒层次的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列内容,并解决问题.
一道习题引发的思考
小明在学习《勾股定理》一章内容时,遇到了一个习题,并对有关内容进行了研究;
习题再现:
古希腊的哲学家柏拉图曾指出,如果![]() 表示大于1的整数,
表示大于1的整数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
资料搜集:
定义:勾股数是指可以构成一个直角三角形三边的一组正整数.一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么
,那么![]() ,
,![]() ,
,![]() 称为一组勾股数.
称为一组勾股数.
关于勾股数的研究:我囯西周初数学家商高在公元前1000年发现了“勾三,股四,弦五”,这组数![]() 是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:
是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() 是互质的奇数.(注:
是互质的奇数.(注:![]() ,
,![]() ,
,![]() 的相同倍数组成的一组数也是勾股数)
的相同倍数组成的一组数也是勾股数)

问题解答:
(1)根据柏拉图的研究,当![]() 时,请直接写出一组勾股数;
时,请直接写出一组勾股数;
(2)若![]() 表示大于1的整数,试证明
表示大于1的整数,试证明![]() 是一组勾股数;
是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,学校教学楼![]() 的后面有一栋宿舍楼
的后面有一栋宿舍楼![]() ,当光线与地面的夹角是
,当光线与地面的夹角是![]() 时,教学楼在宿舍楼的墙上留下高
时,教学楼在宿舍楼的墙上留下高![]() 的影子
的影子![]() ,而当光线与地面夹角是
,而当光线与地面夹角是![]() 时,教学楼顶
时,教学楼顶![]() 在地面上的影子
在地面上的影子![]() 与墙角
与墙角![]() 有
有![]() 的距离(
的距离(![]() ,
,![]() ,
,![]() 在一条直线上).则教学楼
在一条直线上).则教学楼![]() 的高度为________
的高度为________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目: 来源: 题型:
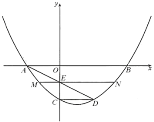
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在抛物线上,且
在抛物线上,且![]() .
.![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 的直线
的直线![]() 平行于
平行于![]() 轴,与抛物线相交于
轴,与抛物线相交于![]() ,
,![]() 两点,则线段
两点,则线段![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:将函数l的图象绕点P(m,0)旋转180°,得到新的函数l'的图象,我们称函数l'是函数关于点P的相关函数.
例如:当m=1时,函数y=(x+1)2+5关于点P(1,0)的相关函数为y=﹣(x﹣3)2﹣5.
(1)当m=0时
①一次函数y=x﹣1关于点P的相关函数为 ;
②点(![]() ,﹣
,﹣![]() )在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
)在二次函数y=﹣ax2﹣ax+1(a≠0)关于点P的相关函数的图象上,求a的值.
(2)函数y=(x﹣1)2+2关于点P的相关函数y=﹣(x+3)2﹣2,则m= ;
(3)当m﹣1≤x≤m+2时,函数y=x2﹣mx﹣![]() m2关于点P(m,0)的相关函数的最大值为6,求m的值.
m2关于点P(m,0)的相关函数的最大值为6,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com