
科目: 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,现将抛物线
,现将抛物线![]() 沿
沿![]() 轴翻折,并向左平移1个单位长度后得到物线
轴翻折,并向左平移1个单位长度后得到物线![]() .
.
(1)求抛物线![]() 的解析式.
的解析式.
(2)若抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 右侧),点
右侧),点![]() 在抛物线
在抛物线![]() 对称轴上一点,
对称轴上一点,![]() 为坐标原点,则抛物线
为坐标原点,则抛物线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是干行四边形?若存在,求出点
为顶点的四边形是干行四边形?若存在,求出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
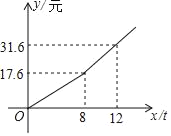
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水8吨以内(包括8吨)和用水8吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
(1)求出自来水公司在这两个用水范围内的收费标准;
(2)若芳芳家6月份共交水费28.1元,请写出用水量超过8吨时应交水费y(元)与用水量x(吨)之间的函数关系,并求出芳芳家6月份的用水量.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着天气的逐渐炎热(如图1),遮阳伞在我们的日常生活中随处可见如图2所示,遮阳伞立柱OA垂直于地面,当将遮阳伞撑开至OD位置时,测得∠ODB=45°,当将遮阳伞撑开至OE位置时,测得∠OEC=30°,且此时遮阳伞边沿上升的竖直高度BC为20cm,求若当遮阳伞撑开至OE位置时伞下阴凉面积最大,求此时伞下半径EC的长.(结果保留根号)

查看答案和解析>>
科目: 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
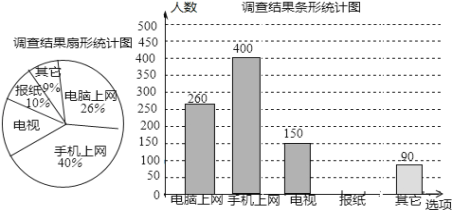
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是 ;请补全条形统计图;
(2)扇形统计图中,“电视”所对应的圆心角的度数是 ;
(3)若该市约有90万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数。
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,点M,N在同一个正比例函数图象上的是( )
A.M(2,﹣3),N(﹣4,6)B.M(﹣2,3),N(4,6)
C.M(﹣2,﹣3),N(4,﹣6)D.M(2,3),N(﹣4,6)
查看答案和解析>>
科目: 来源: 题型:
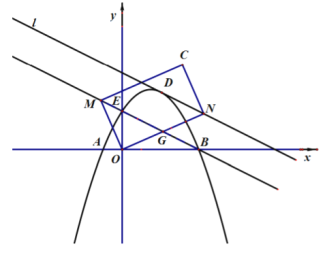
【题目】已知:如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 点和
点和![]() 点(
点(![]() 点在
点在![]() 点左则),交
点左则),交![]() 轴于
轴于![]() 点,作直线
点,作直线![]() 是直线
是直线![]() 上方抛物线上的一个动点.过
上方抛物线上的一个动点.过![]() 点作 直线
点作 直线![]() 平行于直线
平行于直线![]() 是直线
是直线 ![]() 上的任意点,
上的任意点,![]() 是直线
是直线![]() 上的任意点,连接
上的任意点,连接![]() ,始终保持
,始终保持![]() 为
为![]() ,以
,以![]() 和
和![]() 边,作矩形
边,作矩形![]() .
.
(1)在![]() 点移动过程中,求出当
点移动过程中,求出当![]() 的面积最大时点
的面积最大时点![]() 的坐标;在
的坐标;在![]() 的面积最大 时,求矩形
的面积最大 时,求矩形![]() 的面积的最小值.
的面积的最小值.
(2)在![]() 的面积最大时,线段
的面积最大时,线段![]() 交直线
交直线![]() 于点
于点![]() ,当点
,当点![]() 四个点组成平行 四边形时,求此时线段
四个点组成平行 四边形时,求此时线段![]() 与抛物线的交点坐标.
与抛物线的交点坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】材料:解形如(x+a)4+(x+b)4=c的一元四次方程时,可以先求常数a和b的均值![]() ,然后设y=x+
,然后设y=x+![]() .再把原方程换元求解,用种方法可以成功地消去含未知数的奇次项,使方程转化成易于求解的双二次方程,这种方法叫做“均值换元法.
.再把原方程换元求解,用种方法可以成功地消去含未知数的奇次项,使方程转化成易于求解的双二次方程,这种方法叫做“均值换元法.
例:解方程:(x﹣2)4+(x﹣3)4=1
解:因为﹣2和﹣3的均值为![]() ,所以,设y=x﹣
,所以,设y=x﹣![]() ,原方程可化为(y+
,原方程可化为(y+![]() )4+(y﹣
)4+(y﹣![]() )4=1,
)4=1,
去括号,得:(y2+y+![]() )2+(y2﹣y+
)2+(y2﹣y+![]() )2=1
)2=1
y4+y2+![]() +2y3+
+2y3+![]() y2+
y2+![]() y+y4+y2+
y+y4+y2+![]() ﹣2y3+
﹣2y3+![]() y2﹣
y2﹣![]() y=1
y=1
整理,得:2y4+3y2﹣![]() =0(成功地消去了未知数的奇次项)
=0(成功地消去了未知数的奇次项)
解得:y2=![]() 或y2=
或y2=![]() (舍去)
(舍去)
所以y=±![]() ,即x﹣
,即x﹣![]() =±
=±![]() .所以x=3或x=2.
.所以x=3或x=2.
(1)用阅读材料中这种方法解关于x的方程(x+3)4+(x+5)4=1130时,先求两个常数的均值为______.
设y=x+____.原方程转化为:(y﹣_____)4+(y+_____)4=1130.
(2)用这种方法解方程(x+1)4+(x+3)4=706
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司销售两种椅子,普通椅子价格是每把180元,实木椅子的价格是每把400元.
(1)该公司在2019年第一月销售了两种椅子共900把,销售总金额达到了272000元,求两种椅了各销售了多少把?
(2)第二月正好赶上市里开展家俱展销活动,公司决定将普通椅子每把降30元后销售,实木椅子每把降价2a%(a>0)后销售,在展销活动的第一周,该公司的普通椅子销售量比上一月全月普通椅子的销售量多了![]() a%:实木椅子的销售量比第一月全月实木椅子的销售量多了a%,这一周两种椅子的总销售金额达到了251000元,求a的值.
a%:实木椅子的销售量比第一月全月实木椅子的销售量多了a%,这一周两种椅子的总销售金额达到了251000元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com