
科目: 来源: 题型:
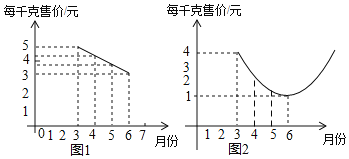
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
查看答案和解析>>
科目: 来源: 题型:
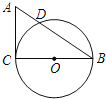
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,有4张除了正面图案不同,其余都相同的卡片,将这4张卡片背面朝上混匀.
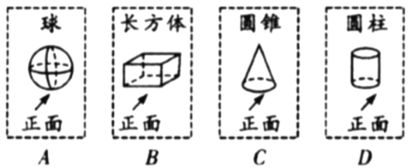
(1)若淇淇从中抽一张卡片,求抽到的卡片上所示的立体图形的主视图为矩形的概率;
(2)若嘉嘉先从中随机抽出一张后放回并混匀,淇淇再随机抽出一张,请用列表法或画树状图求两人抽到的卡片上所示的立体图形的主视图都是矩形的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
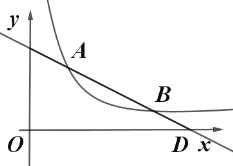
(1)求直线和反比例函数的解析式;
(2)若直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,嘉淇认为
,嘉淇认为![]() ,请通过计算说明她的观点是否正确.
,请通过计算说明她的观点是否正确.
查看答案和解析>>
科目: 来源: 题型:
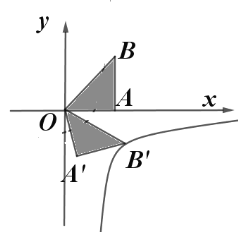
【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,将
,将![]() 绕顶点
绕顶点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,使点
,使点![]() 落在双曲线
落在双曲线![]() 的图象上,则
的图象上,则![]() ________,该双曲线的函数解析式为________.
________,该双曲线的函数解析式为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中点
中点![]() 、
、![]() 是某函数图象上任意两点
是某函数图象上任意两点![]() .将函数图象中
.将函数图象中![]() 的部分沿直线
的部分沿直线![]() 作轴对称,
作轴对称,![]() 的部分沿直线
的部分沿直线![]() 作轴对称,与原函数图象中
作轴对称,与原函数图象中![]() 的部分组成了个新函数的图象,称这个新函数为原函数关于点
的部分组成了个新函数的图象,称这个新函数为原函数关于点![]() 、
、![]() 的“双对称函数”.
的“双对称函数”.
例如:如图①,点![]() 、
、![]() 是一次函数
是一次函数![]() 图象上的两个点,则函数
图象上的两个点,则函数![]() 关于点
关于点![]() 、
、![]() 的“双对称函数”的图象如图②所示.
的“双对称函数”的图象如图②所示.
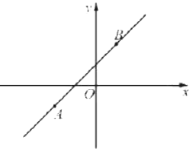
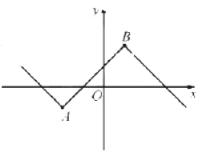
图① 图②
(1)点![]() 、
、![]() 是函数
是函数![]() 图象上的两点,
图象上的两点,![]() 关于点
关于点![]() 、
、![]() 的“双对称函数”的图象记作
的“双对称函数”的图象记作![]() .若
.若![]() 是中心对称图形,直接写出
是中心对称图形,直接写出![]() 的值.
的值.
(2)点![]() 、
、![]() 是二次函数
是二次函数![]() 图象上的两点,该二次函数关于点
图象上的两点,该二次函数关于点![]() 、
、![]() 的“双对称函数”记作
的“双对称函数”记作![]() .
.
①求![]() 、
、![]() 两点的坐标(用含
两点的坐标(用含![]() 的代数式表示).
的代数式表示).
②当![]() 时,求出函数
时,求出函数![]() 的解析式;
的解析式;
③若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 时,
时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 为
为![]() 中点.动点
中点.动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,点
运动,点![]() 关于点
关于点![]() 对称点为点
对称点为点![]() ,以
,以![]() 为边向上作正方形
为边向上作正方形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
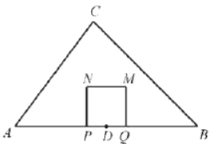
(1)当![]() _______秒时,点
_______秒时,点![]() 落在
落在![]() 边上.
边上.
(2)设正方形![]() 与
与![]() 重叠部分面积为
重叠部分面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)当正方形![]() 的对角线所在直线将
的对角线所在直线将![]() 的分为面积相等的两部分时,直接写出
的分为面积相等的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 和
和![]() 是有公共顶点的直角三角形,
是有公共顶点的直角三角形,![]() ,点
,点![]() 为射线
为射线![]() ,
,![]() 的交点.
的交点.
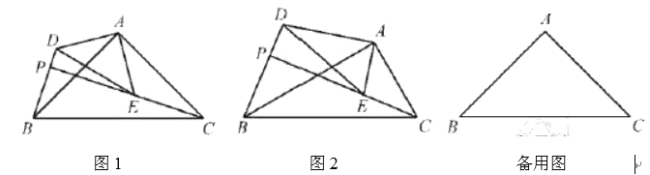
(1)如图1,若![]() 和
和![]() 是等腰三角形,求证:
是等腰三角形,求证:![]() ;
;
(2)如图2,若![]() ,问:(1)中的结论是否成立?请说明理.
,问:(1)中的结论是否成立?请说明理.
(3)在(1)的条件下,![]() ,
,![]() ,若把
,若把![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,请直接写出
时,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com