
科目: 来源: 题型:
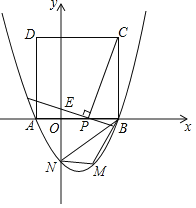
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在
为边在![]() 轴上方作正方形
轴上方作正方形![]() ,点
,点![]() 是
是![]() 轴上一动点,连接
轴上一动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线与
的垂线与![]() 轴交于点
轴交于点![]() .
.
(1)求该抛物线的函数关系表达式;
(2)当点![]() 在线段
在线段![]() (点
(点![]() 不与
不与![]() 重合)上运动至何处时,线段
重合)上运动至何处时,线段![]() 的长有最大值?并求出这个最大值;
的长有最大值?并求出这个最大值;
(3)在第四象限的抛物线上任取一点![]() ,连接
,连接![]() .请问:
.请问:![]() 的面积是否存在最大值?若存在,求出此时点
的面积是否存在最大值?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
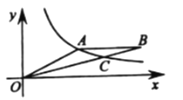
【题目】如图,![]() 是反比例函数
是反比例函数![]() 在第一象限图像上一点,连接
在第一象限图像上一点,连接![]() ,过
,过![]() 作
作![]() 轴,截取
轴,截取![]() (
(![]() 在
在![]() 右侧),连接
右侧),连接![]() ,交反比例函数
,交反比例函数![]() 的图像于点
的图像于点![]() .
.
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求点![]() 的坐标及
的坐标及![]() 所在直线解析式;
所在直线解析式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】从共享单车,共享汽车等共享出行到共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速的普及,根据国家信息中心发布的中国分享经济发展报告2017显示,参与共享经济活动超6 亿人,比上一年增加约1亿人.
(1)为获得北京市市民参与共享经济活动信息,下列调查方式中比较合理的是 ;
A.对某学校的全体同学进行问卷调查
B.对某小区的住户进行问卷调查
C.在全市里的不同区县,选取部分市民进行问卷调查
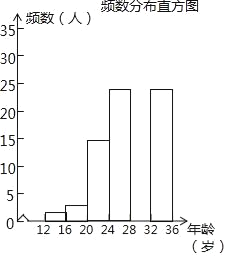
(2)调查小组随机调查了延庆区市民骑共享单车情况,某社区年龄在12~36岁的人有1000人,从中随机抽取了100人,统计了他们骑共享单车的人数,并绘制了如下不完整的统计图表.如图所示.骑共享单车的人数统计表
年龄段(岁) | 频数 | 频率 |
12≤x<16 | 2 | 0.02 |
16≤x<20 | 3 | 0.03 |
20≤x<24 | 15 | a |
24≤x<28 | 25 | 0.25 |
28≤x<32 | b | 0.30 |
32≤x<36 | 25 | 0.25 |
根据以上信息解答下列问题:
①统计表中的a= ;b= ;
②补全频数分布直方图;
③试估计这个社区年龄在20岁到32岁(含20岁,不含32岁)骑共享单车的人有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目: 来源: 题型:
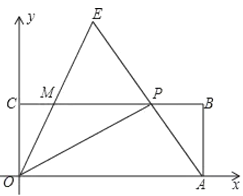
【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当x为何值时,OP⊥AP?
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
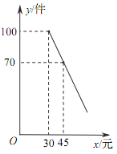
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料,解决问题:
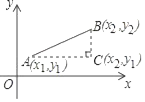
如图,为了求平面直角坐标系中任意两点A(x1,y1)、B(x2,y2)之间的距离,可以AB为斜边作Rt△ABC,则点C的坐标为C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,根据勾股定理可得AB=![]() ,反之,可以将代数式
,反之,可以将代数式![]() 的值看做平面内点(x1,y1)到点(x2,y2)的距离.
的值看做平面内点(x1,y1)到点(x2,y2)的距离.
例如∵![]() =
=![]() =
=![]() ,可将代数式
,可将代数式![]() 看作平面内点(x,y)到点(﹣1,3)的距离
看作平面内点(x,y)到点(﹣1,3)的距离
根据以上材料解决下列问题
(1)求平面内点M(2,﹣3)与点N(﹣1,3)之间的距离;
(2)求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC, 交AB的延长线于E,垂足为F.
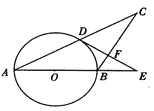
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
(1)求证:AB=CE;
(2)若![]() ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com