
科目: 来源: 题型:
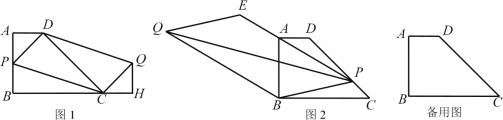
【题目】已知在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=4,BC=6.
(1)如图1,P为AB边上一点,以PD,PC为边作平行四边形PCQD,过点Q作QH⊥BC,交BC的延长线于H.求证:△ADP≌△HCQ;
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE.请问对角线PQ的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
(3)如图2,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE,PB为边作平行四边形PBQE.请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某宾馆有客房90间,当每间客房的定价为每天140元时,客房会全部住满.当每间客房每天的定价每涨10元时,就会有5间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出60元的各种费用.
(1)请写出该宾馆每天入住的客房数y(间)与每间客房涨价x(元)(x为10的倍数)满足的函数关系式;
(2)请求出该宾馆一天的最大利润,并指出此时客房定价应为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,连结OD,AD.以下结论:①∠ADB=90°;②D是BC的中点;③AD是∠BAC的平分线;④OD∥AC,其中正确结论的个数有( )
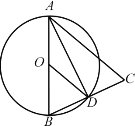
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下: 
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于![]() ;
;
所以图中![]() 即为所求的点.(1)在图②中,连接
即为所求的点.(1)在图②中,连接![]() ,说明∠
,说明∠![]() =30°
=30°
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(深入探究)
(3)已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为________.
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,二次函数y=mx 2 +2mx-4(m≠0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为(-2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标;
查看答案和解析>>
科目: 来源: 题型:
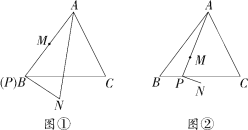
【题目】如图,在△ABC中,AB=BC=10,tan∠ABC=![]() ,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
(1)如图①,当点P在点B,点M是AP中点时,试求AN的长;
(2)如图②,当![]() =
=![]() 时,
时,
①求点N到BC边的距离(用含t的代数式表示);
②当点P从点B运动至点C时,试求点N运动路径的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业接到一批防护服生产任务,按要求15天完成,已知这批防护服的出厂价为每件80元,为按时完成任务,该企业动员放假回家的工人及时返回加班赶制.该企业第![]() 天生产的防护服数量为
天生产的防护服数量为![]() 件,
件,![]() 与
与![]() 之间的关系可以用图中的函数图象来刻画.
之间的关系可以用图中的函数图象来刻画.

(1)直接写出![]() 与
与![]() 的函数关系式________;
的函数关系式________;
(2)由于疫情加重,原材料紧缺,防护服的成本前5天为每件50元,从第6天起每件防护服的成本比前一天增加2元,设第![]() 天创造的利润为
天创造的利润为![]() 元,直接利用(1)的结论,求
元,直接利用(1)的结论,求![]() 与
与![]() 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)
查看答案和解析>>
科目: 来源: 题型:
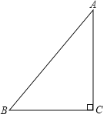
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为检测“停课不停学”期间九年级学生的复习情况,进行了中考数学模拟测试并从中随机抽取了部分学生的测试成绩分成![]() 个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
个小组,根据每个小组的人数绘制如图所示的尚不完整的频数分布直方图.
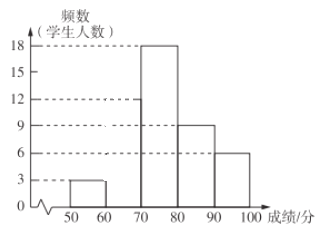
请根据信息回答下列问题:
![]() 若成绩在
若成绩在![]() 分的频率为
分的频率为![]() ,请计算抽取的学生人数并补全频数分布直方图;
,请计算抽取的学生人数并补全频数分布直方图;
![]() 在此次测试中,抽取学生成绩的中位数在______ 分数段中;
在此次测试中,抽取学生成绩的中位数在______ 分数段中;
![]() 若该校九年级共有
若该校九年级共有![]() 名学生,成绩在
名学生,成绩在![]() 分以上的(含
分以上的(含![]() 分)为优秀,请通过计算说明,大约有多少名学生在本次测试中数学成绩为优秀.
分)为优秀,请通过计算说明,大约有多少名学生在本次测试中数学成绩为优秀.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com