
科目: 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
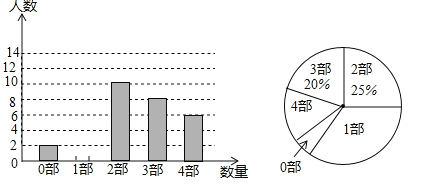
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)该药店计划一次购进两种型号的口罩共2000只,其中B型口罩的进货量不超过A型口罩的3倍,设购进A型口罩x只,这2000只口罩的销售总利润为y元.
①求y关于x的函数关系式;
②该药店购进A型、B型口罩各多少只,才能使销售总利润最大?
(3)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,决定把B型口罩的售价调整为进价的15%,求B型口罩降价的幅度.
查看答案和解析>>
科目: 来源: 题型:
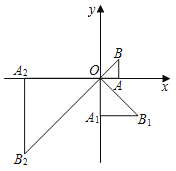
【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋90°转得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O,…,依此规律,得到等腰直角三角形A2020OB2020,则点B2020的坐标为_____.
查看答案和解析>>
科目: 来源: 题型:
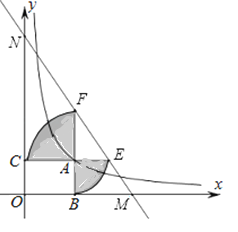
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目: 来源: 题型:
【题目】受新冠疫情影响,3月1日起,“君乐买菜”网络公司某种蔬菜的销售价格开始上涨.如图1,前四周该蔬菜每周的平均销售价格y(元/kg)与周次x(x是正整数,1≤x<5)的关系可近似用函数![]() 刻画;进入第5周后,由于外地蔬菜的上市,该蔬菜每周的平均销售价格y(元/kg)从第5周的6元/kg下降至第6周的5.6元/kg,y与周次x(5≤x≤7)的关系可近似用函数
刻画;进入第5周后,由于外地蔬菜的上市,该蔬菜每周的平均销售价格y(元/kg)从第5周的6元/kg下降至第6周的5.6元/kg,y与周次x(5≤x≤7)的关系可近似用函数![]() 刻画.
刻画.
(1)求a,b的值.
(2)若前五周该蔬菜的销售量m(kg)与每周的平均销售价格y(元/kg)之间的关系可近似地用如图2所示的函数图象刻画,第6周的销售量与第5周相同:
①求m与y的函数表达式;
②在前六周中,哪一周的销售额w(元)最大?最大销售额是多少?

(3)若该蔬菜第7周的销售量是100kg,由于受降雨的影响,此种蔬菜第8周的可销售量将比第7周减少a%(a>0).为此,公司又紧急从外地调运了5吨此种蔬菜,刚好满足本地市民的需要,且使此种蔬菜第8周的销售价格比第7周仅上涨0.8a%.若在这一举措下,此种蔬菜在第8周的总销售额与第7周刚好持平,请通过计算估算出a的整数值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
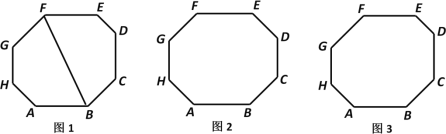
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
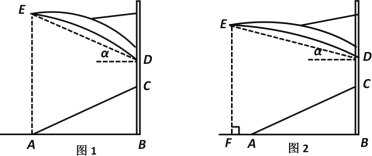
(1)求观众区的水平宽度AB.
(2)求图1中点E离水平地面的高度EA.
(3)因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校七年级甲班、乙班举行一分钟投篮比赛,每班派10名学生参赛,在规定时间内进球数不少于8个为优秀学生.比赛数据的统计图表如下(数据不完整):
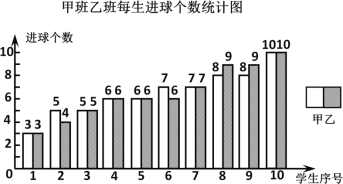

根据以上信息,解答下列问题:
(1)直接写出a,b,c的值.
(2)你认为哪个班的比赛成绩要好一些?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com