
科目: 来源: 题型:
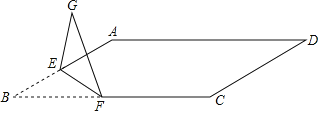
【题目】如图,在ABCD中,AB=6,BC=6![]() ,∠D=30°,点E是AB边的中点,点F是BC边上一动点,将△BEF移沿直线EF折叠,得到△GEF,当FG∥AC时,BF的长为_____.
,∠D=30°,点E是AB边的中点,点F是BC边上一动点,将△BEF移沿直线EF折叠,得到△GEF,当FG∥AC时,BF的长为_____.
查看答案和解析>>
科目: 来源: 题型:
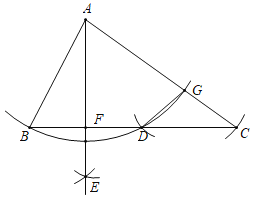
【题目】如图,在△ABC中,∠B=2∠C,以点A为圆心,AB长为半径作弧,交BC于点D,交AC于点G;再分别以点B和点D为圆心,大于![]() BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
BD的长为半径作弧,两弧相交于点E,作射线AE交BC于点F,若以点G为圆心,GC长为半径作两段弧,一段弧过点C,而另一段弧恰好经过点D,则此时∠FAC的度数为( )
A.54°B.60°C.66°D.72°
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线C的解析式为y=x2+2x﹣3,C与x轴交于点A,B(点A在点B左侧),与y轴交于点D,顶点为P.
(Ⅰ)求点A,B,D,P的坐标;
(Ⅱ)若将抛物线C沿着直线PD的方向平移得到抛物线C′;
①当抛物线C′与直线y=2x﹣5只有一个公共点时,求抛物线C′的解析式;
②点M(xm,ym)是①中抛物线C′上一点,若﹣6≤xm≤2且ym为整数,求满足条件的点M的个数.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,点A(4,0),点B(0,4),C是AB中点,连接OC,将△AOC绕点A顺时针旋转,得到△AMN,记旋转角为α,点O,C的对应点分别是M,N.连接BM,P是BM中点,连接OP,PN.
(Ⅰ)如图①.当α=45°时,求点M的坐标;
(Ⅱ)如图②,当α=180°时,求证:OP=PN且OP⊥PN;
(Ⅲ)当△AOC旋转至点B,M,N共线时,求点M的坐标(直接写出结果即可).

查看答案和解析>>
科目: 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校初级中学数学兴趣小组为了解本校学生年龄情况,随机调查了本校部分学生的年龄,根据所调查的学生的年龄(单位:岁),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受调查的学生人数为_______,图①中 ![]() 的值为 ;
的值为 ;
(2)求统计的这组学生年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目: 来源: 题型:
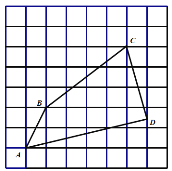
【题目】如图,在每个小正方形的边长为的网格中,点![]() 均在格点上,
均在格点上,![]() 为小正方形边中点.
为小正方形边中点.
(1)![]() 的长等于 ______;
的长等于 ______;
(2)请在如图所示的网格中,用无刻度的直尺,画出一个点![]() ,使其满足
,使其满足![]() 说明点
说明点![]() 的位置是如何找到的(不要求证明)______.
的位置是如何找到的(不要求证明)______.
查看答案和解析>>
科目: 来源: 题型:
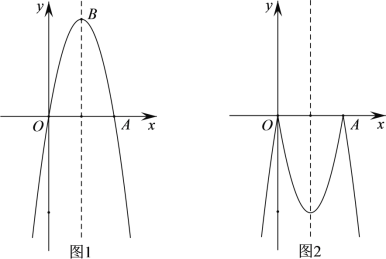
【题目】如图1,已知抛物线C1:![]() 与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:
与x轴的正半轴交于点A,点B为抛物线的顶点,直线l:![]() 是一条动直线.
是一条动直线.
(1)求点A、点B的坐标;
(2)当直线l经过点A时,求出直线l的解析式,并直接写出此时当![]() 时,自变量x的取值范围;
时,自变量x的取值范围;
(3)如图2,将抛物线C1在x轴上方的部分沿x轴翻折,与C1在x轴下方的图形组合成一个新的图形C2,当直线l与组合图形C2有且只有两个交点时,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com