
科目: 来源: 题型:
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB,CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°,求建筑物CD的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AC平分∠BAD,∠ABC=60°,E为AD上一点,AE=2,DE=4,P为AC 上一点,则△PDE周长的最小值为_______.
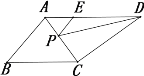
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=![]() x+1的图象与二次函数y=
x+1的图象与二次函数y=![]() x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
x2+bx+c的图象交于A,B两点,点A在x轴上.点B的横坐标为4.
(1)b= ,c= ;
(2)设二次函数的图象与y轴交于C点,与x轴的另一个交点为D.连接AC,CD,求∠ACD的正弦值;
(3)若M点在x轴下方二次函数图象上,
①过M点作y轴平行线交直线AB于点E,以M点为圆心,ME的长为半径画圆,求圆M在直线AB上截得的弦长的最大值;
②若∠ABM=∠ACO,则点M的坐标为 .
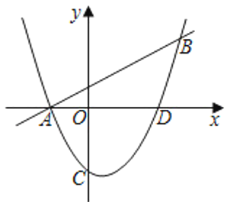
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B在x轴上,点C在y轴上,AB=BC=5,AC=8,D为线段AB上一动点,以CD为边在x轴上方作正方形CDEF,连接AE.
(1)若点B的坐标为(m,0),则m= ;
(2)当BD= 时,EA⊥x轴;
(3)当点D由点B运动到点A过程中,点F经过的路径长为 ;
(4)当△ADE面积最大时,求出BD的长及△ADE面积最大值.
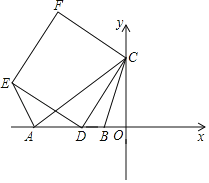
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,线段AB经过⊙O的圆心O,交⊙O于A、C两点,BC=1,AD为⊙O的弦,连结BD,∠BAD=∠ABD=30°.
(1)求证:直线BD是⊙O的切线;
(2)求⊙O的半径长.
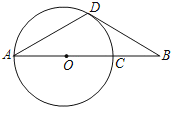
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了解九年级学生新冠疫情防控期间每天居家体育活动的时间(单位:![]() ),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
),在网上随机调查了该校九年级部分学生.根据调查结果,绘制出如下的统计图1和图2.请根据相关信息,解答下列问题:
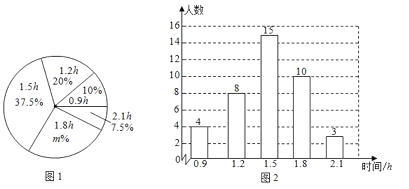
(1)本次接受调查的初中学生人数为________,图①中![]() 的值为________;
的值为________;
(2)这组数据的平均数是________,众数是________,中位数是________;
(3)根据统计的这组每天居家体育活动时间的样本数据,估计该校500名九年级学生居家期间每天体育活动时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com