
科目: 来源: 题型:
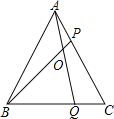
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
查看答案和解析>>
科目: 来源: 题型:
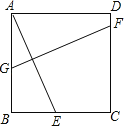
【题目】如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
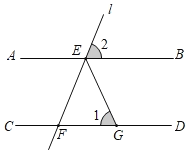
【题目】如图,AB∥CD,点E是直线AB上的点,过点E的直线l交直线CD于点F,EG平分∠BEF交CD于点G.在直线l绕点E旋转的过程中,图中∠1,∠2的度数可以分别是( )
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:有一组对角互补的四边形叫做互补四边形.
![]() 概念理解:
概念理解:
①在互补四边形![]() 中,
中,![]() 与
与![]() 是一组对角,若
是一组对角,若![]() 则
则![]() _
_ ![]()
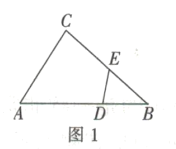
②如图1,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,且
上,且![]() 求证:四边形
求证:四边形![]() 是互补四边形.
是互补四边形.
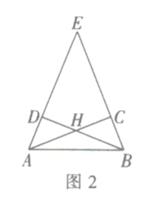
![]() 探究发现:如图2,在等腰
探究发现:如图2,在等腰![]() 中,
中,![]() 点
点![]() 分别在边
分别在边![]() 上,
上, ![]() 四边形
四边形![]() 是互补四边形,求证:
是互补四边形,求证:![]() .
.
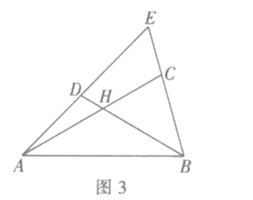
![]() 推广运用:如图3,在
推广运用:如图3,在![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() 四边形
四边形![]() 是互补四边形,若
是互补四边形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
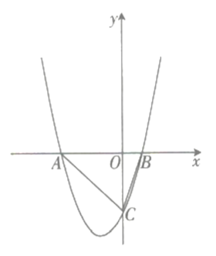
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() 的面积为
的面积为![]() .
.
①求这条抛物线相应的函数解析式.
②在拋物线上是否存在一点![]() 使得
使得![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() .若
.若![]() 设
设 ![]() (当点
(当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为
的值为![]() ),
),![]() .
.
小明根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.
![]() 通过取点、画图、计算,得到了
通过取点、画图、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
说明:补全表格时,相关数值保留一位小数.
(参考数据:![]() ) .
) .
![]() 如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
如图2,描出剩余的点,并用光滑的曲线画出该函数的图象.
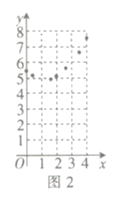
![]() 观察图象,下列结论正确的有 _ .
观察图象,下列结论正确的有 _ .
①函数有最小值,没有最大值
②函数有最小值,也有最大值
③当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
④当![]() 时,
时,![]() 随着
随着![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目: 来源: 题型:
【题目】如今,不少人在购买家具时追求简约大气的风格,图1所示的是一款非常畅销的简约落地收纳镜,其支架的形状固定不变,镜面可随意调节,图2所示的是其侧面示意图,其中![]() 为镜面,
为镜面,![]() 为放置物品的收纳架,
为放置物品的收纳架,![]() 为等长的支架,
为等长的支架,![]() 为水平地面,已知
为水平地面,已知![]() ,
,![]() .(结果精确到
.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
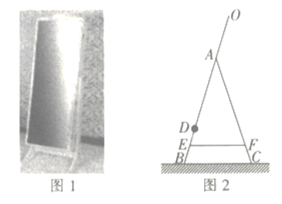
(1)求支架顶点![]() 到地面
到地面![]() 的距离.
的距离.
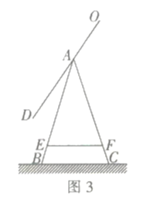
(2)如图3,将镜面顺时针旋转![]() 求此时收纳镜顶部端点
求此时收纳镜顶部端点![]() 到地面
到地面![]() 的距离.
的距离.
查看答案和解析>>
科目: 来源: 题型:
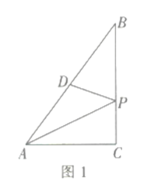
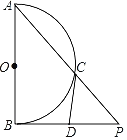
【题目】如图,已知AB为半圆O的直径,过点B作PB⊥OB,连接AP交半圆O于点C,D为BP上一点,CD是半圆O的切线.
(1)求证:CD=DP.
(2)已知半圆O的直径为![]() ,PC=1,求CD的长.
,PC=1,求CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|

请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在网格纸中,![]() 、
、![]() 都是格点,以
都是格点,以![]() 为圆心,
为圆心,![]() 为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
为半径作圆,用无刻度的直尺完成以下画图:(不写画法)
(1)在圆①中画圆![]() 的一个内接正六边形
的一个内接正六边形![]() ;
;
(2)在图②中画圆![]() 的一个内接正八边形
的一个内接正八边形![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com